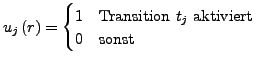Petrinetze

Definition

Petrinetz

$PN=\left(P,T,A,M'\right)$

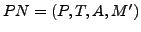
• Gerichteter, bipartiter Graph - mit 2 Arten von Knoten (Plätzen und Transitionen)
• Zeichnung siehe Abbildung cap:Petrinetz-Grundelemente

  Figure: Petrinetz Grundelemente

  

Plätze

$P=\left\{ p_{1},\ldots,p_{n}\right\}$

• beschreiben mögliche Zustände, Darstellung als Kreis
• Englisch: places

Transitionen

$T=\left\{ t_{1},\ldots,t_{m}\right\}$

• beschreiben mögliche Ereignisse, Darstellung als Rechteck

gerichtete Kanten

$A=\left\{ \left(a_{1},a_{1}'\right),\ldots,\left(a_{k},a_{k}'\right)\right\}$

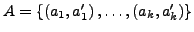
• Verbinden Plätze und Transitionen
• Englisch: directed edges

Markierungen

$M=\left(m_{1},\ldots,m_{n}\right)\in\mathbb{N}^{n}$

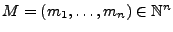
• definieren den aktuellen Zustand des Petrinetzses mit
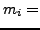  $m_{i}=$ Anzahl der Markierungen in Platz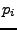 $p_{i}$
• werden in Plätzen gespeichert, Darstellung als schwarze Punkte im Kreis
• Anfangsmarkierung $M'$
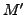
• Englisch: tokens

dynamik eines Petrinetzes

ist wie folgt charakterisiert

• Markierungen werden erzeugt, gelöscht oder verschoben durch Schalten von Transitionen (firing of transitions)
• Transition ist Schaltbereit (bzw. aktiviert) wenn alle ihre Eingangsplätze markiert sind (bzw. mind. eine Marke enthalten)
• Schaltbereite Transitionen können schalten (feuern), wobei eine Marke aus jedem Eingangsplatz weggenommen und in jedem Ausgangsplatz eine Marke hinzugefügt wird.
• Feuern ist im allgemeinen ein nichtdeterministischer Vorgang

Typen

von Petrinetzen

Zeidiskrete

(kausale) Modelle: Petrinetz beschreibt logisch, was in welcher Sequenz passiert

Zeitkontinuierliche

Modelle: zusätzliche Vorhersage, wann ein Ereigniss auftritt.

Stochastische

Petrinetze: zufallsverteilte Verzögerungsdauern der Schaltregeln

Mathematische Darstellung zeitdiskreter Petrinetze

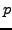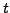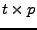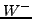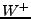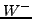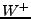Die Struktur eines Petrinetzes mit $p$ Plätzen und $t$ Transitionen kann durch zwei $t\times p$-Matrizen $W^{-}$und $W^{+}$ dargestellt werden. In $W^{-}$ werden für alle Verbindungen eines Platze mit einer Transition (in dieser Reihenfolge / pre-weights) 1en und sonst 0en eingetragen. In $W^{+}$ werden für alle Verbindungen einer Transition mit einem Platz (in dieser Reihenfolge / post-weights) 1en und sonst 0en eingetragen. Die Inzidenzmatrix ergibt sich wie folgt

$$W=W^{+}-W^{-}$$

Simulation zeitdiskreter Petrinetze

Markierungsvektor

zum Zeitpunkt $r$

$$m\left(r\right)=\left(m_{1}\left(r\right),\ldots,m_{n}\left(r\right)\right)^{T}$$

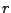
Kapazitätsvektor

$k=\left(k_{1},\ldots,k_{n}\right)^{T}$

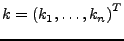
• Es soll gelten 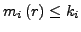$m_{i}\left(r\right)\le k_{i}$ für $i\in\left\{ 1,\ldots,n\right\}$

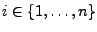
Aktivierungsfunktion

$$u_{j}\left(r\right)=\begin{cases} 1 & \textrm{Transition }t_{j}\textrm{ aktiviert}\\ 0 & \textrm{sonst}\end{cases}$$

• In allen ``Vor-Plätzen'' müssen hinreichend viele Markierungen verfügbar sein
• In allen ``Nach-Plätzen'' darf die maximale Kapazität nach Schalten der Transition nicht überschritten werden

Schaltfunktion

$m\left(r\right)=m\left(r-1\right)+W\cdot u\left(r\right)$

Charakteristika von Petrinetzen

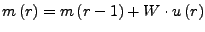
Erreichbarkeit (Reachability)

• Ein Zustand heißt erreichbar von einem Anfangszustand, falls es eine Sequenz vom Anfangszustand zu diesem exisitert
• Der Erreichbarkeitsgraph (Graph mit möglichen zuständen des Petrinetzes als Knoten und mit Transitionen beschrifteten gerichteten Kanten dazwischen.
  • ob gewünschte Zustände erreicht, bzw. unerwünschte Zustände nicht erreicht werden können
  • ob Vorgägner gefährlicher Zustände umgangen werden können
• ist NP Hart in Speicher und Zeit

Beschränktheit

• Ein Petrinetz heißt beschränkt (bounded), falls in keinem Platz (zu keinem Zeitpunkt) mehr als eine gewisse Maximalanzahl von 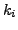$k_{i}$ Markierungen vonhanden ist.
• Falls 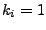$k_{i}=1$, nennt man das Petrinetz sicher (safe)

Verklemmung (Deadlock)

• Eine Verklemmung (deadlock) eines Petrinetzes ist eine Transition (oder eine Menge von Transitionen), die nicht schalten können.
• Diese können nie schalten.

Lebendigkeit (Liveness)

• Eine Transition heißt tod (dead, non-live), falls sie bei keiner Folgemarkierung mehr aktivierbar ist.
• Diese kann nicht mehr schalten.