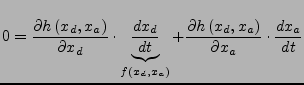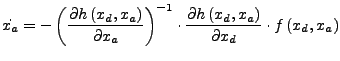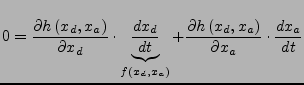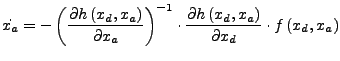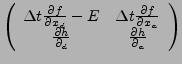Next: Index
Up: Modulare Modellbildung und Simulation
Previous: Modulare Modellbildung
Contents
Index
Subsections
- Bisher betrachtete Bewegungsgleichungen eines dynamischen Systems
- basieren auf einem minimalen Satz von Zustandsvariablen (Minimalkoordinaten)
- führen auf Systeme gewöhnlicher DGLn (ordinary differential equations,
ODEs), die numerisch effiziernt integriert werden
können
- aber nicht alle Systeme sind leicht in Minimalkoordinaten formulierbar
- Rechnergestützte, modulare Modellierung
- führt auf Systeme differential-algebraischer Gleichungen (DAEs)
- Integration von DAEs ist aufwendiger als von ODEs
- DGLn mit Nebenbedingungen
- benötigt konsistente Anfangswerte, d.h.
- Totale Differentiation der Nebenbedingung nach der Zeit
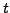
- Wenn Jakobimatrix von
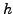 nach
nach 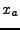 invertierbar ist, kann formal
nach
invertierbar ist, kann formal
nach 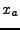 aufgelöst werden
aufgelöst werden
- Mit dieser und der Gleichung
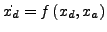 erhält man so wieder eine ODE die wie bisher gelöst werden kann
erhält man so wieder eine ODE die wie bisher gelöst werden kann
- Kriterium für die Schwierigkeit der numerischen Lösung einer DAE ist
der sogenannte Index
- Es gibt verschiedene Index-Definitionen. Wichtigster und häufigster
ist:
Differentieller Index 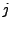 einer DAE ist die kleinste Anzahl der nötigen
Differentiationen, so dass
explizit nach
einer DAE ist die kleinste Anzahl der nötigen
Differentiationen, so dass
explizit nach
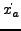 auflösbar ist.
auflösbar ist.
- Je größer des Index ist, um so schwieriger ist die numerische Integration!
- Möglichkeit der Bifurkation (Verzweigung)
der Lösung
Drift
- Bei numerischer unvermeidlicher Abweichung von exakter Lösung für
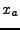 ``driftet'' die numerische Lösung ab
``driftet'' die numerische Lösung ab
- Abhilfe: (impliziter) Prädiktor/Korrektor-Ansatz
- Impliziter Ansatz (z.B. Euler)
- Numerische Lösung mit Newton-Verfahren nach
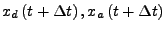
- Benötigt Invertierbarkeit der entsprechenden Jakobimatrix:
- Vorraussetzung: Index 1
- DAEs vonhöherem Index müssen auf Index 1 reduziert werden
- Einbettung in steifes ODE-System für
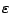 sehr klein
sehr klein
- Untersuchung von (implizieten) Runge-Kutta und Extrapolationsverfahren
für Grenzfall
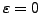 liefern effiziente und zuverlässige
DAE-Integratoren
liefern effiziente und zuverlässige
DAE-Integratoren
- Sehr verbreitet sind auch implizite Mehrschrittverfahren: z.B.: BDF-Verfahren,
DASSL
- Hierbei handelt es sich um einen bipartiten Graphen mit gerichteten
und ungerichteten Kanten
- Für jede Gleichung wird das Gleichungsymbol in einen Kreis geschrieben
und als Knoten verwendet
- Für jede in den Gleichungen vorkommende Variable gibt es einen Knoten
(aber ohne Umkreisung)
- Die gerichteten Kanten zwischen den Variablen und Gleichungen deuteten
an, dass die Gleichung nach dieser Variablen auflösbar ist
- Falls eine Variable zwar in einer Gleichung vorkommt, diese aber nicht
nach ihr auflösbar ist, wird eine ungerichtete Kante verwendet
- Alle Variablen, von denen mindestens zwei Formeln abhängen und mindestens
eine Formel nach auflösbar ist lassen sich durch Gleichsetzen oder
Einsetzen eliminieren
- Interessante Fragestellung: Lässt sich diesem Graphen der Index ansehen?
- System``schaltbild''
- DAE-System
- Elinination der Potential und Flussgleichungen
- vereinfachtes DAE-System
- Index-1-DAE-System
- Partition und Schleifenreduktion
- vereinfachtes Index1-DAE-System
- numerische Lösung





Next: Index
Up: Modulare Modellbildung und Simulation
Previous: Modulare Modellbildung
Contents
Index
Marco Möller 17:20:55 24.10.2005