Schallwellen

Ausbeitung

in allen elastischen Medien. Entspricht einer Dichteschwankung im Medium

Dichtegradient

$\frac{\partial\varrho}{\partial x}=-\varrho\frac{\partial^{2}\xi^{2}}{\partial x^{2}}$

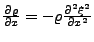
Druckgradient

$\frac{\partial p}{\partial x}=-\left(\frac{dp}{d\varrho}\right)_{\varrho_{0}}\varrho\frac{d^{2}\xi}{dx^{2}}$

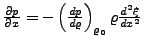
Wellengleichung

$\frac{\partial^{2}\xi}{dt^{2}}=\left(\frac{dp}{d\varrho}\right)_{\varrho_{0}}\frac{\partial^{2}\xi}{\partial x^{2}}$

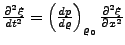
Lösung

$\xi=\xi_{0}\sin\left(\omega t-kx\right)$

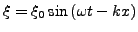
Ausbreitungsgeschwindigkeit

$v^{2}=\left(\frac{dp}{d\varrho}\right)_{\varrho_{0}}$

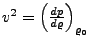
Schallwellen

Longitudinalwellen in Luft

Schallwellendruck

$p=\frac{\textrm{Kraft}}{\textrm{Fläche}}$

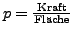
Energietransport

$P_{v}=\frac{\textrm{Kraft}}{\textrm{Fläche}}\cdot\frac{\textrm{Weg}}{\textrm{Zeit}}=\frac{\textrm{Leistung}}{\textrm{Fläche}}$

Schallintensität

$\frac{\textrm{Energie}}{\textrm{Zeit}\cdot\textrm{Fläche}}$

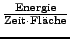
Standardintensität

$J_{o}=10^{-6}\frac{W}{cm^{2}}$

• Schmerzgrenze $J_{max}\approx10^{13}J_{0}$
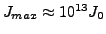
• Wahrnehmungsschwelle $J_{min}\approx10^{-10}J_{0}$

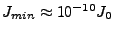
Lautstärke

$L\sim\textrm{konst}\cdot\log J$

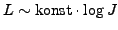
• Alte Einheit Phon:
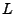  $L$ in Phon $=10\cdot\log_{10}\left(\frac{J}{J_{0}}\right)$

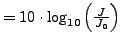
Tonhöhe

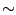$\sim$ Frequenz

Schallwellen in Gasen

Polarisation

Nur Longitudinal möglich, da Gase keine Schersteifigkeit besitzen.

Ideales Gas

entspicht einem Abiabaten Prozess, da er schnell abläuft

Ausbreitunggeschwindigkeit

$v_{schall}=\sqrt{\kappa\frac{kT}{m}}$

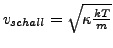
• nur für ideales Gas
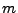• $m$ Molmasse
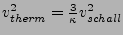• $v_{therm}^{2}=\frac{3}{\kappa}v_{schall}^{2}$ also ähnliche Größe
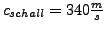• $c_{schall}=340\frac{m}{s}$ bei Norm Bedingungen

Akustik

Ton

Schallempfindung, die durch harmonische Schwingung des Schallgeber erzeugt wird

Klang

Schallempfindung regelmäßiger harmonischer Schwingungsvorgänge mit rationalem Frequenzspektrum

Geräusch

kein rationales Frequenzspektrum

Schwebung

Überlagerung zweier Töne mit annähern gleichen Frequenzen

• $x_{1}=x_{0}\sin\left(\omega_{1}t\right)$
  $x_{2}=x_{0}\sin\left(\omega_{2}t\right)$
• $\omega_{1}\approx\omega_{2}$
• $x=x_{1}+x_{2}=x_{0}\left(\sin\left(\omega_{1}t\right)+\sin\left(\omega_{2}t\right)\right)$
• $x=2\cdot x_{0}\cdot\sin\left(\frac{\omega_{1}+\omega_{2}}{2}t\right)\cdot\cos\left(\frac{\omega_{1}-\omega_{2}}{2}t\right)$
• $x=2\cdot x_{0}\cdot\sin\left(\omega_{m}t\right)\cdot\cos\left(\omega_{s}t\right)$
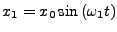
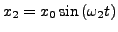
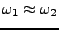
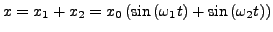
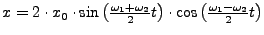
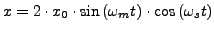
• Mittenfrequenz $\omega_{m}=\frac{\omega_{1}+\omega_{2}}{2}$
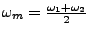
• Schwebungsfreqzenz $\omega_{s}=\left\vert\frac{\omega_{1}-\omega_{2}}{2}\right\vert$
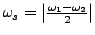
• Hat Phasensprünge an stellen wo der Sinus und der Cosinus gleich 0 werden

Dispersion

Phasengeschwindigkeit

$\frac{dx}{dt}=\frac{\omega}{k}=v_{phase}$

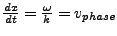
• wegen $\omega t-kx=\textrm{konstant}$

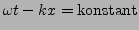
Gruppengeschwindigkeit

ist die Geschwindigkeit mit der bei Überlagerung von mehreren Harmonischen Wellen sich die Umhüllende Kurve Vortbewegt.

• im Medien mit $v_{phase}=v\left(\lambda\right)$
• $v_{gr}=v_{phase}-\lambda\frac{dv_{phase}}{d\lambda}=\frac{d\omega}{dk}$

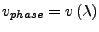
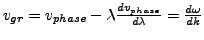
Dispersion

die Abhängigkeit der Ausbreitungsgeschwindigkeit von Wellen von ihrer Wellenlänge bzw. von der Frequenz

linear

$v_{gruppe}=v_{phase}=\textrm{konst}$

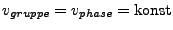
nichtlinear

$v_{phase}\neq\textrm{konst}$

• $v_{gruppe}=\frac{\partial\omega}{\partial k}\neq v_{phase}$
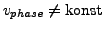
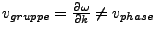
• Signal behält seine Form bei der Ausbreitung nicht bei, dies führt zu einer Deformation (Dispersion) des Signals

• Wasserwelle $p_{ph}=v=\sqrt{\frac{\lambda g}{2\pi}}=v\left(\lambda\right)$
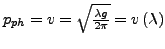
  • Im Fernfeld des Erregers überholen die langen Wellen die Kürzeren