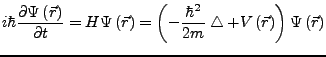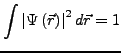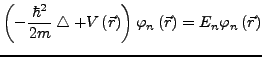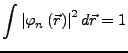Verallgemeinerungen

Kinetische Energie

$T=\frac{\vec{p}^{2}}{2m}=\frac{1}{2m}\left(p_{x}^{2}+p_{y}^{2}+p_{z}^{2}\right)$

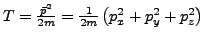
• klassisch 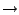$\rightarrow$ qm: $q_{i}\rightarrow\frac{\hbar}{i}\frac{d}{dx_{i}}$

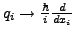
Schrödinger Gleichung

$$i\hbar\frac{\partial\Psi\left(\vec{r}\right)}{\partial t}=H\Psi\l... ...bar^{2}}{2m}\bigtriangleup+V\left(\vec{r}\right)\right)\Psi\left(\vec{r}\right)$$

Statistische Interpretation

$$\int\left\vert\Psi\left(\vec{r}\right)\right\vert^{2}d\vec{r}=1$$

Für zeitunabhängige Potentiale

vereinfacht sich dies zu

$$\Psi\left(\vec{r}\right)=\varphi_{n}\left(\vec{r}\right)\cdot e^{-\frac{i}{\hbar}E_{n}t}$$

$$\left(-\frac{\hbar^{2}}{2m}\bigtriangleup+V\left(\vec{r}\right)\right)\varphi_{n}\left(\vec{r}\right)=E_{n}\varphi_{n}\left(\vec{r}\right)$$

$$\int\left\vert\varphi_{n}\left(\vec{r}\right)\right\vert^{2}d\vec{r}=1$$

Kommutatoren

zwischen Ort und Impuls

• $\left[r_{i},p_{i}\right]=i\hbar\delta_{ij}$
• $\left[r_{i},r_{j}\right]=\left[p_{i},p_{j}\right]=0$

Ehrenfest Theorem

$$\frac{d}{dt}\left\langle \vec{r}\right\rangle = \frac{1}{m}\left\langle \vec{p}\right\rangle$$

$$\frac{d}{dt}\left\langle \vec{p}\right\rangle = \left\langle -\vec{\nabla}V\right\rangle$$

Harmonische Oszillator in 3d

$$\varphi_{n}\left(\vec{r}\right)=\varphi_{nx}\left(x\right)\cdot\varphi_{ny}\left(y\right)\cdot\varphi_{nz}\left(z\right)$$

Entartete Zustände

liegen vor, wenn es zu einem Energiewert mehrere Eigenzustände existieren.