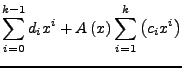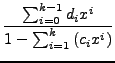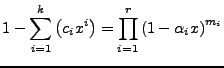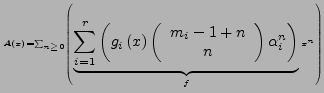Next: Graphentheorie
Up: Rekursionen
Previous: Lineare Rekursionsgleichungen
Contents
Index
Subsections
Erzeugende Funktionen
Sei
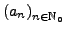 eine Folge.
Die formale Potenzreihe
eine Folge.
Die formale Potenzreihe
heißt erzeugende Funktion zur Folge
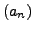 .
.
Sind
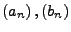 zwei Folgen mit entsprechenden
Funktionen
zwei Folgen mit entsprechenden
Funktionen
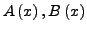 , dann:
, dann:
- Summe
-
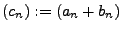
Hat erzeugende Funktion
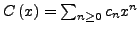 und wir schreiben
und wir schreiben
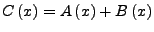
- Produkt
-
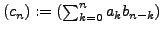
Hat erzeugende Funktion
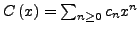 und wir schreiben
und wir schreiben
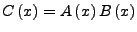
- Erzeugende Funktionen lassen sich gliedweise Integrieren
und Differenzieren, um so neue erzeugende Funktionen
zu konstruieren.
Inverse
Sei
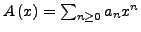 erzeugende Funktion
zu
erzeugende Funktion
zu
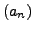 . Dann heißt die erzeugende Funktion
. Dann heißt die erzeugende Funktion
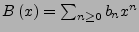 invers zu
invers zu
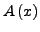 , falls
, falls
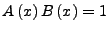
- Hier ist
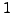 die erzeugende Funktion zur Folge
die erzeugende Funktion zur Folge
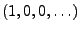
- Die erzeugende Funktion
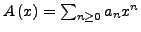 hat eine inverse erzeugende Funktion (auch:
hat eine inverse erzeugende Funktion (auch:
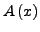 ist
invertierbar) genau dann, wenn
ist
invertierbar) genau dann, wenn
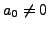
- geometrische Reihe
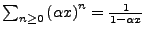
-
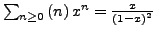
-
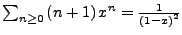
-
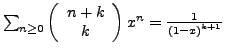
-
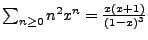
-
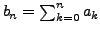 die Folgen zu den erzeugenden Funktionen
die Folgen zu den erzeugenden Funktionen
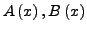
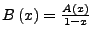
- Gegeben
- ist eine lineare Rekursionsgleichung
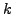 -ter Ordnung
-ter Ordnung
- Ansatz
- (Siehe Algorithmus 1 auf der nächsten Seite) Hierbei ersetzt
man
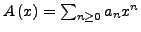 durch die Rekursionsdefinition.
Dabei entstehen Terme die wieder nur ein
durch die Rekursionsdefinition.
Dabei entstehen Terme die wieder nur ein 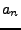 mit verschobenen
Summationsbereich enthalten. Hier kann man nun durch Umformung das
ganze wieder in ein Polynom plus
mit verschobenen
Summationsbereich enthalten. Hier kann man nun durch Umformung das
ganze wieder in ein Polynom plus
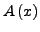 bringen.
bringen.
![\begin{algorithm*}
% latex2html id marker 687
[th]
\par
\caption{: Ansatz zum Lö...
...\right)\right)+c_{k}x^{k}A\left(x\right)$
\end{description}\par
\end{algorithm*}](img210.png)
- Koeffizienten Zusammenfassen
- (aus letzter Gleichung) zu
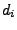
- Faktorisieren des Nenners
- (Bestimmen von
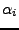 und
und 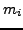 )
)
- Partialbruchbruchzerlegung
- (Bestimmen von
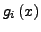 )
)
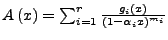
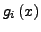 wird von
wird von 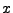 unabhängig, wenn beim Faktorisieren
des Nenners komplexe Lösungen zugelassen werden. Dies erleichtert
die Anwendung des nächsten Punktes.
unabhängig, wenn beim Faktorisieren
des Nenners komplexe Lösungen zugelassen werden. Dies erleichtert
die Anwendung des nächsten Punktes.
- Erstellen von Erzeugenden Funktion
- für
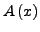
- Koeffizientenvergleich
-
Wenn alle 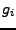 nicht von
nicht von 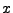 abhängig sind, so ist
abhängig sind, so ist 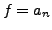 ,
wenn nicht muss diese Formel noch etwas umgestellt werden. Hiermit
wäre ein geschlossener Ausdruck für
,
wenn nicht muss diese Formel noch etwas umgestellt werden. Hiermit
wäre ein geschlossener Ausdruck für 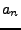 gefunden.
gefunden.





Next: Graphentheorie
Up: Rekursionen
Previous: Lineare Rekursionsgleichungen
Contents
Index
Marco Möller 17:26:01 24.10.2005
![]() eine Folge.
Die formale Potenzreihe
eine Folge.
Die formale Potenzreihe
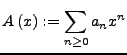
![]() zwei Folgen mit entsprechenden
Funktionen
zwei Folgen mit entsprechenden
Funktionen
![]() , dann:
, dann:
![]() erzeugende Funktion
zu
erzeugende Funktion
zu
![]() . Dann heißt die erzeugende Funktion
. Dann heißt die erzeugende Funktion
![]() invers zu
invers zu
![]() , falls
, falls
![]()
![\begin{algorithm*}
% latex2html id marker 687
[th]
\par
\caption{: Ansatz zum Lö...
...\right)\right)+c_{k}x^{k}A\left(x\right)$
\end{description}\par
\end{algorithm*}](img210.png)