




Next: Entwicklung nach einer Zeile/Spalte
Up: Determinanten I.241
Previous: Determinanten I.241
Contents
Index
Subsections
Permutation / Transposition
I.241
Eine bijektive Abbildung
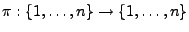 heißt Permutation der Menge
heißt Permutation der Menge
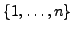 . Die Menge
aller Permutationen von
. Die Menge
aller Permutationen von
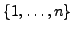 wird mit
wird mit 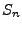 bezeichnet.
bezeichnet.
Mit 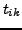 bezeichnen wir die Permutation
bezeichnen wir die Permutation
eine Transposition (vertauschen zweier Elemente).
Notation für Permutation:
-
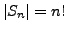
- jede Permutation kann als Hintereinanderausführung von Transpositionen
geschrieben werden
Fehlstand / Signum I.242
Sei
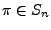 . Gilt
. Gilt
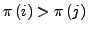 für
zwei Zahlen
für
zwei Zahlen
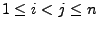 , so heißt das Paar
, so heißt das Paar
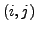 Fehlstand von
Fehlstand von 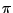 .
.
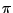 heißt gerade (ungerade), falls
heißt gerade (ungerade), falls 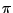 eine gerade
(ungerade) Anzahl von Fehlstellen hat.
eine gerade
(ungerade) Anzahl von Fehlstellen hat.
Das Signum von 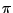 ist
ist
- eine gerade (ungerade) Permutation kann nur durch eine gerade (ungerade)
Anzahl von hintereinander ausgeführten Transpositionen dargestellt
werden.
-
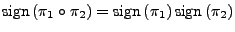
-
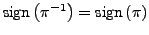
Determinante I.244
Sei
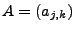 eine
eine 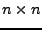 -Matrix mit Elementen
aus
-Matrix mit Elementen
aus
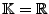 oder
oder
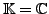 . Dann heißt
. Dann heißt
Determinante von  (Definition nach Leibnitz
Formel) mit folgender Schreibweise:
(Definition nach Leibnitz
Formel) mit folgender Schreibweise:
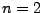
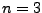 (Regel von Sarrus)
(Regel von Sarrus)
Man schreibe die Linke und Mittlere Spalte Rechts noch einmal daneben.
Die 3 Diagonalen von Linksoben nach Rechtsunten werden nun multipliziert
und mit positiven Vorzeichen addiert. Die 3 Diagonalen von Rechtsoben
nach Linksunten mit werden nun multipliziert und mit negativen Vorzeichen
dazuaddiert.
- Da Berechnungsformel in
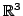 dem Spatprodukt entspricht,
bezeichnet man die Determinante auch mit Volumenform.
dem Spatprodukt entspricht,
bezeichnet man die Determinante auch mit Volumenform.
- bei größeren
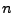 macht es keinen Sinn geschlossene Ausdrücke Anzugeben,
da die Anzahl der Terme mit
macht es keinen Sinn geschlossene Ausdrücke Anzugeben,
da die Anzahl der Terme mit 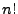 wächst.
wächst.
- Bei Matrizen in Dreiecksgestalt (Ober- oder Unterhalb der Hauptdiagonale
nur 0en) ist
-
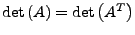
-
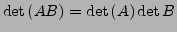
-
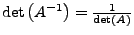
-
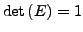
- bei komplexkonjungierten Zahlen:
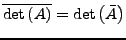
Verhalten von Determinante bei Zeilen-
und Spaltenoperationen I.246
Schreiben
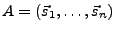 (
(
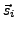 Spaltenvektor). Die Determinante stellt eine alternierende
Multilinearform
dar.
Spaltenvektor). Die Determinante stellt eine alternierende
Multilinearform
dar.
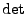 ist in jedem Argument linear:
ist in jedem Argument linear:
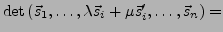
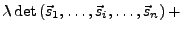
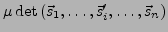
für jeden Index
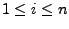
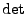 ist alternierend:
ist alternierend:
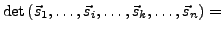
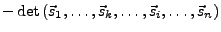
für
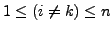
Analog gelten diese Aussagen auch für Zeilenoperationen.
Der Algorithmus erfolgt hier wie bei der Bestimmung von Rängen. Ziel
ist es die Determinante in eine Dreiecksgestalt zu bringen. Dann entspricht
die Determinante dem Produkt der Hauptdiagonale. Allerdings ist Folgendes
zu berücksichtigen:
- Zeilen- und Spaltenoperationen erlaubt, ändern aber zum Teil (berechenbar)
den Wert der Determinante.
- Hat
 zwei gleiche Spalten (Zeilen), so ist
zwei gleiche Spalten (Zeilen), so ist 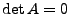
- Addition mit einem Vielfachen einer anderen Spalte (Zeile)
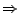 unverändert:
unverändert:
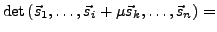
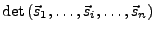 wenn
wenn 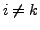
- Multiplikation einer Spalte (Zeile) mit
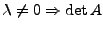 mit
mit 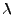 multiplizieren:
multiplizieren:
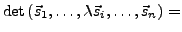
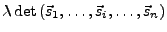
- Vertauschen zweier Spalten (Zeilen) ändert Vorzeichen von
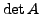 :
:
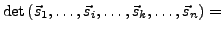
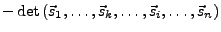
Determinante und Rang I.248
Der Rang einer 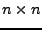 -Matrix
-Matrix  ist genau dann gleich
ist genau dann gleich 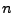 (
( ist regulär), wenn
ist regulär), wenn
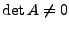 ist.
ist.





Next: Entwicklung nach einer Zeile/Spalte
Up: Determinanten I.241
Previous: Determinanten I.241
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() heißt Permutation der Menge
heißt Permutation der Menge
![]() . Die Menge
aller Permutationen von
. Die Menge
aller Permutationen von
![]() wird mit
wird mit ![]() bezeichnet.
bezeichnet.
![]() bezeichnen wir die Permutation
bezeichnen wir die Permutation
![]() . Gilt
. Gilt
![]() für
zwei Zahlen
für
zwei Zahlen
![]() , so heißt das Paar
, so heißt das Paar
![]() Fehlstand von
Fehlstand von ![]() .
.
![]() heißt gerade (ungerade), falls
heißt gerade (ungerade), falls ![]() eine gerade
(ungerade) Anzahl von Fehlstellen hat.
eine gerade
(ungerade) Anzahl von Fehlstellen hat.
![]() ist
ist
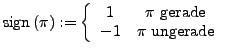
![]() eine
eine ![]() -Matrix mit Elementen
aus
-Matrix mit Elementen
aus
![]() oder
oder
![]() . Dann heißt
. Dann heißt
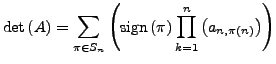
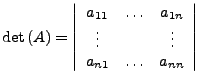
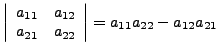
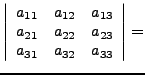
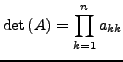
![]() (
(
![]() Spaltenvektor). Die Determinante stellt eine alternierende
Multilinearform
dar.
Spaltenvektor). Die Determinante stellt eine alternierende
Multilinearform
dar.
![]() -Matrix
-Matrix ![]() ist genau dann gleich
ist genau dann gleich ![]() (
(![]() ist regulär), wenn
ist regulär), wenn
![]() ist.
ist.