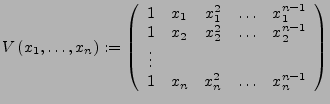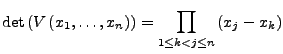Next: Die Cramersche Regel I.259
Up: Determinanten I.241
Previous: Definitionen
Contents
Index
Subsections
Adjunkte I.256
Sei
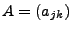 eine
eine 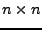 -Matrix. Durch Streichen
der
-Matrix. Durch Streichen
der 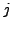 -ten Zeile und
-ten Zeile und 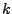 -ten Spalte entsteht die
-ten Spalte entsteht die
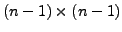 -Matrix.
-Matrix.
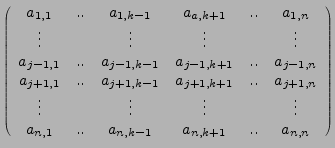
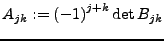 heißt Adjunkte
des Eintrages
heißt Adjunkte
des Eintrages 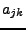 .
.
Entwickeln nach einer Zeile oder Spalte I.256
Sei
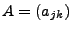 eine
eine 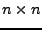 -Matrix. Dann gilt
-Matrix. Dann gilt
- Am besten nach Spalte (Zeile) mit sehr vielen 0-en entwickeln
- Evtl. auch mischen mit Gauß Algorithmus
Vandermonde-Matrix I.258
Seien
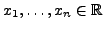 (oder
(oder
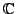 ).
).
heißt Vandermonde-Matrix in
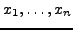 . Es gilt
. Es gilt
Marco Möller 17:42:11 24.10.2005
![]() eine
eine ![]() -Matrix. Durch Streichen
der
-Matrix. Durch Streichen
der ![]() -ten Zeile und
-ten Zeile und ![]() -ten Spalte entsteht die
-ten Spalte entsteht die
![]() -Matrix.
-Matrix.
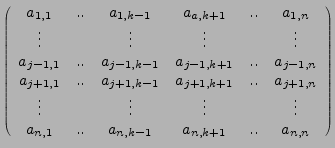
![]() heißt Adjunkte
des Eintrages
heißt Adjunkte
des Eintrages ![]() .
.
![]() eine
eine ![]() -Matrix. Dann gilt
-Matrix. Dann gilt


![]() (oder
(oder
![]() ).
).