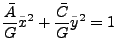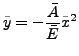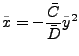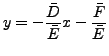Next: Index
Up: Drehung im und Quadriken
Previous: Gebilde
Contents
Index
Subsections
Überführen von allgemeine Quadriken in Normalform
Eine Gleichung der Form
ist eine Quadrik in allgemeiner Form.
Gegeben ist eine Quadrik in allgemeiner Form. Diese lässt dich nun
so drehen, das der gemischte Term (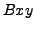 ) verschwindet, die Gleichung
also die Form
) verschwindet, die Gleichung
also die Form
mit 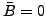 hat. Hierzu wird mit dem Winkel
hat. Hierzu wird mit dem Winkel
gedreht.
-
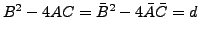 bleibt unberührt von der
Drehung.
bleibt unberührt von der
Drehung.
mit
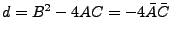
- Ellipse
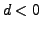
- Parabel
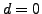
- Hyperbel
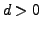
Gegeben ist eine Quadrik in der Form:
Bei dieser wurde also bereits der gemischte Term ``weggedreht''.
- Hyperbel, Ellipse
- falls
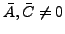 :
:
- Parabel
- falls
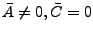 :
:
- Parabel
- falls
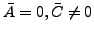 :
:
- Gerade
- falls
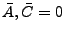 :
:





Next: Index
Up: Drehung im und Quadriken
Previous: Gebilde
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() ) verschwindet, die Gleichung
also die Form
) verschwindet, die Gleichung
also die Form
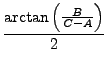
![]()