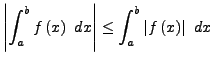Next: Taylorentwicklung II.141
Up: Integralrechnung II.92
Previous: Flächen- und Stammfunktion /
Contents
Index
Subsections
Uneigentliche
Integrale II.131
Unter uneigentlichen Integralen versteht man uneingeschränkte Integrale
(z.B.
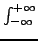 ) oder Integrale über uneingeschränkte
Funktionen (z.B.
) oder Integrale über uneingeschränkte
Funktionen (z.B.
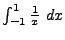 ).
).
Sei
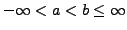 und
und
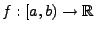 .
Für alle Teilintervalle
.
Für alle Teilintervalle
![$ \left[\alpha,\beta\right]\subset\left[a,b\right)$](img680.png) existiert das Riemannsche Integral. Die Funktion heißt uneigentlich
integrierbar auf
existiert das Riemannsche Integral. Die Funktion heißt uneigentlich
integrierbar auf
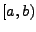 , wenn
, wenn
existiert. Entsprechend
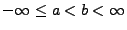 :
Wenn beide Grenzen unbeschränkt sind, lässt sich dies durch Zerlegung
des Integrationsbereiches lösen.
:
Wenn beide Grenzen unbeschränkt sind, lässt sich dies durch Zerlegung
des Integrationsbereiches lösen.
Majorrantenkriterium II.133
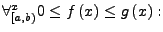 Konvergiert
das uneigentliche Integral
Konvergiert
das uneigentliche Integral
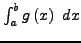 , so
auch
, so
auch
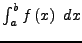 und es gilt
und es gilt
- Hilft beim abschätzen, ob es eine Lösung geben kann, und in welchen
Intervall sie liegen wird.
Betragskriterium II.134
Wenn
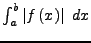 konvergiert
konvergiert
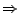 Konvergenz von
Konvergenz von
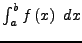 und es gilt
und es gilt
Marco Möller 17:42:11 24.10.2005
![]() ) oder Integrale über uneingeschränkte
Funktionen (z.B.
) oder Integrale über uneingeschränkte
Funktionen (z.B.
![]() ).
).
![]() und
und
![]() .
Für alle Teilintervalle
.
Für alle Teilintervalle
![]() existiert das Riemannsche Integral. Die Funktion heißt uneigentlich
integrierbar auf
existiert das Riemannsche Integral. Die Funktion heißt uneigentlich
integrierbar auf
![]() , wenn
, wenn
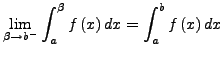
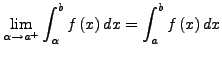
![]() Konvergiert
das uneigentliche Integral
Konvergiert
das uneigentliche Integral
![]() , so
auch
, so
auch
![]() und es gilt
und es gilt
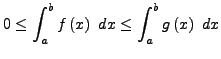
![]() konvergiert
konvergiert
![]() Konvergenz von
Konvergenz von
![]() und es gilt
und es gilt