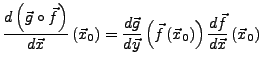Next: Lokale Extrema
Up: Differenzierbare Funktionen im II.219
Previous: Differenzierbare Funktionen im II.219
Contents
Index
Subsections
Sei
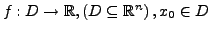 ein innerer Punkt von
ein innerer Punkt von 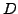 .
.  heißt differenzierbar in
heißt differenzierbar in
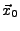 ,
wenn es ein
,
wenn es ein
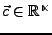 und eine Funktion
und eine Funktion
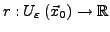 gibt mit
gibt mit
und
gilt. Dies entspricht einer linearen Approximierbarkeit
von  .
.
Funktionalmatrix oder Jacobimatrix
II.223
Sei
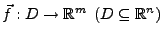 eine Funktion,
eine Funktion,
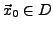 ein innerer Punkt.
ein innerer Punkt.
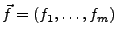 heißt in
heißt in
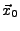 differenzierbar, falls alle Komponentenfunktionen
differenzierbar, falls alle Komponentenfunktionen
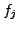 differenzierbar sind.
differenzierbar sind.
heißt Funktionalmatrix oder Jacobimatrix von 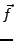 in
in
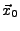 .
.
- Zeilen der Jacobimatrix = Gradienten der Komponentenfunktionen.
Differenzierbarkeit mehrdimensionaler Funktion
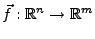 wenn:
wenn:
Kettenregel II.225
Sei
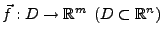 ,
,
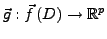 ,
,
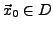 innerer Punkt,
innerer Punkt,
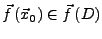 innerer Punkt. Sind
innerer Punkt. Sind  in
in
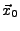 und
und 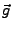 in
in
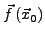 differenzierbar, so ist die Verkettung
differenzierbar, so ist die Verkettung
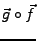 in
in
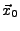 differenzierbar mit
differenzierbar mit





Next: Lokale Extrema
Up: Differenzierbare Funktionen im II.219
Previous: Differenzierbare Funktionen im II.219
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() ein innerer Punkt von
ein innerer Punkt von ![]() .
. ![]() heißt differenzierbar in
heißt differenzierbar in
![]() ,
wenn es ein
,
wenn es ein
![]() und eine Funktion
und eine Funktion
![]() gibt mit
gibt mit
![]() eine Funktion,
eine Funktion,
![]() ein innerer Punkt.
ein innerer Punkt.
![]() heißt in
heißt in
![]() differenzierbar, falls alle Komponentenfunktionen
differenzierbar, falls alle Komponentenfunktionen
![]() differenzierbar sind.
differenzierbar sind.
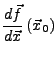
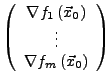
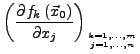
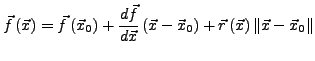
![]() ,
,
![]() ,
,
![]() innerer Punkt,
innerer Punkt,
![]() innerer Punkt. Sind
innerer Punkt. Sind ![]() in
in
![]() und
und ![]() in
in
![]() differenzierbar, so ist die Verkettung
differenzierbar, so ist die Verkettung
![]() in
in
![]() differenzierbar mit
differenzierbar mit