




Next: Implizite Funktionen II.242
Up: Differenzierbare Funktionen im II.219
Previous: Der Differenzierbarkeitsbegriff II.219
Contents
Index
Subsections
Lokale Extrema
Sei
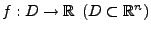 differenzierbar und besitzt
differenzierbar und besitzt  in
in 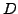 ein relatives Extrema
in
ein relatives Extrema
in
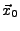 , dann gilt
, dann gilt
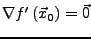 .
.
Quadratische Form / Definit
II.239
Eine quadratische Form auf
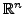 ist eine Abbildung
ist eine Abbildung
für eine symmetrische 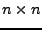 -Matrix
-Matrix  .
.
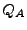 heißt positiv definit (bzw.
negativ definit), wenn
heißt positiv definit (bzw.
negativ definit), wenn
(bzw.
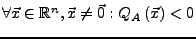 )
gilt.
)
gilt.
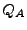 heißt indefinit, falls
heißt indefinit, falls
gilt.
Sei
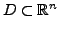 offen,
offen,
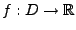 gehört
zu Klasse
gehört
zu Klasse
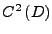 . Im Punkt
. Im Punkt
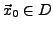 gelte
gelte
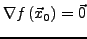 . Dann besitzt
. Dann besitzt  in
in
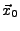 ein relatives Maximum (bzw. Minimum), falls die Hesse-Matrix
ein relatives Maximum (bzw. Minimum), falls die Hesse-Matrix
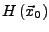 negativ definit (bzw. positiv definit)
ist. Ist
negativ definit (bzw. positiv definit)
ist. Ist
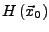 indefinit, so kann
indefinit, so kann  in
in
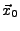 keine Extremalstelle besitzen.
keine Extremalstelle besitzen.
-
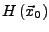 positiv (negativ) definit
positiv (negativ) definit
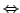 Alle Eigenwerte von
Alle Eigenwerte von
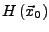 positiv (negativ) sind
positiv (negativ) sind
-
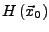 indefinit
indefinit
 Es gibt sowohl positive, als auch negative Eigenwerte
von
Es gibt sowohl positive, als auch negative Eigenwerte
von
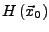
Eine Funktion
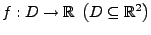 sei in Klasse
sei in Klasse
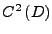 und es gelte
und es gelte
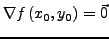 .
Dann gilt mit
.
Dann gilt mit
- Ist
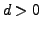 und
und 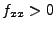
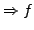 hat relatives Minimum
an
hat relatives Minimum
an
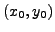
- Ist
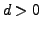 und
und 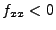
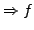 hat relatives Maximum
an
hat relatives Maximum
an
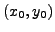
- Ist
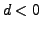
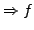 hat kein Extremum an
hat kein Extremum an
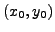





Next: Implizite Funktionen II.242
Up: Differenzierbare Funktionen im II.219
Previous: Der Differenzierbarkeitsbegriff II.219
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() differenzierbar und besitzt
differenzierbar und besitzt ![]() in
in ![]() ein relatives Extrema
in
ein relatives Extrema
in
![]() , dann gilt
, dann gilt
![]() .
.
![]() ist eine Abbildung
ist eine Abbildung
![]() heißt positiv definit (bzw.
negativ definit), wenn
heißt positiv definit (bzw.
negativ definit), wenn
![]() offen,
offen,
![]() gehört
zu Klasse
gehört
zu Klasse
![]() . Im Punkt
. Im Punkt
![]() gelte
gelte
![]() . Dann besitzt
. Dann besitzt ![]() in
in
![]() ein relatives Maximum (bzw. Minimum), falls die Hesse-Matrix
ein relatives Maximum (bzw. Minimum), falls die Hesse-Matrix
![]() negativ definit (bzw. positiv definit)
ist. Ist
negativ definit (bzw. positiv definit)
ist. Ist
![]() indefinit, so kann
indefinit, so kann ![]() in
in
![]() keine Extremalstelle besitzen.
keine Extremalstelle besitzen.
![]() sei in Klasse
sei in Klasse
![]() und es gelte
und es gelte
![]() .
Dann gilt mit
.
Dann gilt mit