Sei
![]() offen, die Funktion
offen, die Funktion
![]() ,
,
![]() (
(![]() -Nebenbedingungsfunktionen
zu Vektor zusammengefasst) mit
-Nebenbedingungsfunktionen
zu Vektor zusammengefasst) mit ![]() seien in
seien in
![]() .
Sei
.
Sei
![]() mit
mit
![]() und
und
![]() (Rang maximal). Weiter sei
(Rang maximal). Weiter sei
![]() ein relatives
Extremum der Menge
ein relatives
Extremum der Menge
![]() dann gibt es
dann gibt es ![]() -Lagrange Multiplikatoren
-Lagrange Multiplikatoren
![]() , so dass
, so dass
![$\displaystyle \forall k\in\left[1,n\right]:f_{x_{k}}\left(\vec{x}_{0}\right)+\sum_{j=1}^{l}\lambda_{j}\left(g_{j}\right)_{x_{k}}\left(\vec{x}_{0}\right)=0$](img850.png)
Sei
![]() , (
, (
![]() offen),
stetig und
offen),
stetig und
![]() , weiter sei
, weiter sei ![]() streng
monoton wachsend (oder fallend) bezgl.
streng
monoton wachsend (oder fallend) bezgl. ![]() (für jedes feste
(für jedes feste ![]() ).
Dann gibt es ein Rechteck
).
Dann gibt es ein Rechteck
Ist ![]() stetig differenzierbar aus
stetig differenzierbar aus ![]() , so ist auch
, so ist auch
![]() stetig differenzierbar in
stetig differenzierbar in ![]() mit
mit
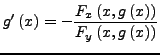
Seien
![]() und
und
![]() offene Mengen. Die Funktionen
offene Mengen. Die Funktionen
![]() gehören der Klasse
gehören der Klasse
![]() an. Sei
an. Sei
![]() mit
mit
![]() und
und
![]() (Jacobi Matrix). Dann gibt es offene Umgebungen
(Jacobi Matrix). Dann gibt es offene Umgebungen
![]() und
und
![]() , so dass für jeden
Punkt
, so dass für jeden
Punkt
![]() genau
ein
genau
ein
![]() mit
mit
![]() existiert.
existiert.