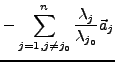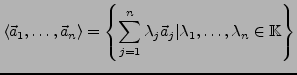Next: Endlich-dimensionale Vektorräume I.166
Up: Vektorräume I.159
Previous: Vektorräume I.159
Contents
Index
Subsections
Sei
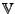 eine Menge und
eine Menge und
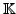 ein Körper.
Zu je zwei Elementen
ein Körper.
Zu je zwei Elementen 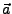 und
und 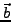 aus
aus
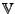 gebe
es genau ein Element
gebe
es genau ein Element
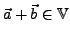 . Zu jedem
. Zu jedem 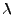 aus
aus
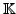 und jedem Element
und jedem Element 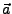 aus
aus
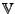 gebe
es genau ein Element
gebe
es genau ein Element
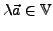 .
.
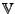 heißt Vektorraum (VR) über
heißt Vektorraum (VR) über
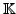 , wenn die folgenden
Grundgesetze gelten.
, wenn die folgenden
Grundgesetze gelten.
Untervektorraum I.160
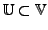 heißt Untervektorraum (UVR)
vom
heißt Untervektorraum (UVR)
vom
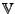 , wenn für
, wenn für
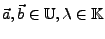 :
:
- Untervektorraumkriterium
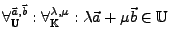
oder
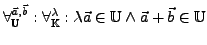
- Durchschnitt
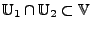
- Vereinigung nicht UVR!!!
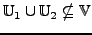
- Summe
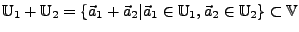
Linearkombination I.161
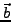 ist eine Linearkombination aus
ist eine Linearkombination aus
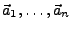 .
.
Triviale Darstellung des
Nullvektors I.162
Lineare (Un-)Abhängigkeit
I.163
Die Vektoren
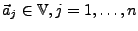 heißen linear
unabhängig wenn sich aus ihnen nur mit der trivialen Darstellung der
Nullvektor darstellen lässt. Ansonsten sind sie Linear abhängig.
heißen linear
unabhängig wenn sich aus ihnen nur mit der trivialen Darstellung der
Nullvektor darstellen lässt. Ansonsten sind sie Linear abhängig.
Bei linear abhängigen Vektoren lässt sich mindestens ein Vektor
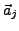 als Linearkombination der restlichen Darstellen:
als Linearkombination der restlichen Darstellen:
- Beweis durch Lösen von lin. Gleichungssystem.
Wenn eindeutig möglich
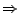 linear unabhängig.
linear unabhängig.
- Anzahl der Vektoren muss
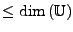 sein,
sonst sind sie zwangsläufig lin. abhängig.
sein,
sonst sind sie zwangsläufig lin. abhängig.
-
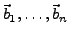 linear unabhängig
linear unabhängig
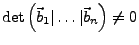
Lineare Hülle I.165
Menge aller Linearkombinationen aus gegebenen Vektoren.
- Die Lineare Hülle bildet einen Untervektorraum von
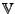
- Wenn
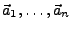 linear unabhängig, und
linear unabhängig, und
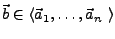 dann ist
dann ist
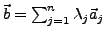 eindeutig.
eindeutig.
- Direkte Summe
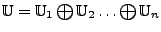
Wenn die Untervektorräume linear unabhängig sind





Next: Endlich-dimensionale Vektorräume I.166
Up: Vektorräume I.159
Previous: Vektorräume I.159
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() eine Menge und
eine Menge und
![]() ein Körper.
Zu je zwei Elementen
ein Körper.
Zu je zwei Elementen ![]() und
und ![]() aus
aus
![]() gebe
es genau ein Element
gebe
es genau ein Element
![]() . Zu jedem
. Zu jedem ![]() aus
aus
![]() und jedem Element
und jedem Element ![]() aus
aus
![]() gebe
es genau ein Element
gebe
es genau ein Element
![]() .
.
![]() heißt Vektorraum (VR) über
heißt Vektorraum (VR) über
![]() , wenn die folgenden
Grundgesetze gelten.
, wenn die folgenden
Grundgesetze gelten.
![]() heißt Untervektorraum (UVR)
vom
heißt Untervektorraum (UVR)
vom
![]() , wenn für
, wenn für
![]() :
:
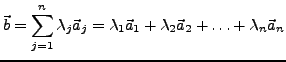
![]() ist eine Linearkombination aus
ist eine Linearkombination aus
![]() .
.
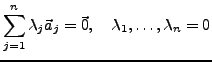
![]() heißen linear
unabhängig wenn sich aus ihnen nur mit der trivialen Darstellung der
Nullvektor darstellen lässt. Ansonsten sind sie Linear abhängig.
heißen linear
unabhängig wenn sich aus ihnen nur mit der trivialen Darstellung der
Nullvektor darstellen lässt. Ansonsten sind sie Linear abhängig.
![]() als Linearkombination der restlichen Darstellen:
als Linearkombination der restlichen Darstellen: