




Next: Koordinaten I.171
Up: Vektorräume I.159
Previous: Definition I.159
Contents
Index
Subsections
Erzeugendensystem I.166
Wenn
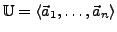 bilden
bilden
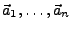 ein Erzeugendensystem von
ein Erzeugendensystem von
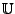 .
.
- Alle Basen sind autom. auch Erzeugendensystem.
Basis I.166
Wenn
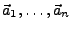 linear unabhängig sind, und
ein Erzeugendensystem von
linear unabhängig sind, und
ein Erzeugendensystem von
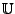 sind bilden sie eine Basis
von
sind bilden sie eine Basis
von
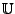 .
.
- Ein Vektor lässt sich in einer Basis eindeutig darstellen
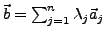
- Es kann unterschiedliche Basen von
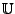 geben.
geben.
- Alle Basen haben die gleiche Anzahl von Vektoren.
- Wenn die Anzahl der Vektoren
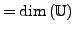 und sie
lin. unabhängig sind, sind sie autom. ein Basis.
und sie
lin. unabhängig sind, sind sie autom. ein Basis.
Kanonische Basis
/ Standardbasis I.169
- Die Standardbasen sind linear unabhängig
- Sie erzeugen
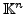
- ist eine Orthonormale Basis (siehe sub:Orthogonalsystem)
Dimension I.167
Die Anzahl von Vektoren von einer Basis wird Dimension genannt:
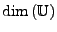
Nullraum I.169
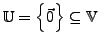 ist ein
trivialer Untervektorraum eines jeden Vektorraumes der Dimension 0.
ist ein
trivialer Untervektorraum eines jeden Vektorraumes der Dimension 0.
Linearer Teilraum I.169
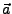 sei ein fester Vektor
sei ein fester Vektor
wird als Linearer Teilraum der
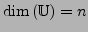 bezeichnet.
bezeichnet.
Die Menge aller geordneten n-Tupel(geordnete Menge an
Zahlen) von Skalaren aus
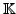 ,
,
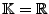 bzw.
bzw.
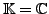
versehen mit der Addition
und der Multiplikation mit Skalaren aus
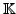 bilden einen n-dimensionalen Vektorraum über
bilden einen n-dimensionalen Vektorraum über
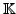 . Dieser
wird mit
. Dieser
wird mit
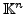 abgekürzt.
abgekürzt.





Next: Koordinaten I.171
Up: Vektorräume I.159
Previous: Definition I.159
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() bilden
bilden
![]() ein Erzeugendensystem von
ein Erzeugendensystem von
![]() .
.
![]() linear unabhängig sind, und
ein Erzeugendensystem von
linear unabhängig sind, und
ein Erzeugendensystem von
![]() sind bilden sie eine Basis
von
sind bilden sie eine Basis
von
![]() .
.
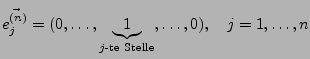
![]()
![]() ist ein
trivialer Untervektorraum eines jeden Vektorraumes der Dimension 0.
ist ein
trivialer Untervektorraum eines jeden Vektorraumes der Dimension 0.
![]() sei ein fester Vektor
sei ein fester Vektor
![]() ,
,
![]() bzw.
bzw.
![]()