Next: Partialbruchzerlegung
Up: Isolierte Singularitäten
Previous: Haupt- und Nebenteil
Contents
Index
Entwicklungssatz von Laurent
Sei
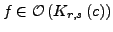 ,
, 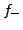 und
und 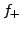 wie in sub:Haupt-und-Nebenteil mit
wie in sub:Haupt-und-Nebenteil mit
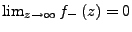 .
Dann gilt
.
Dann gilt
auf
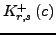 und
auf
und
auf
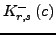 oder kurz
Laurent-Reihe für
oder kurz
Laurent-Reihe für 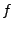 mit Entwicklungspunkt
mit Entwicklungspunkt
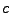 .
.
Beide Reihen konvergieren gleichmäßig auf jeder kompakten Menge 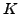 ,
und
,
und
für alle
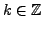 .
.
- Verallgemeinerung von Taylorreihe (siehe sub:Cauchy-Taylor-Entwicklungssatz)
Marco Möller 20:58:46 15.11.2006
![]() ,
, ![]() und
und ![]() wie in sub:Haupt-und-Nebenteil mit
wie in sub:Haupt-und-Nebenteil mit
![]() .
Dann gilt
.
Dann gilt
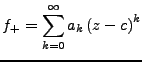
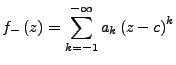
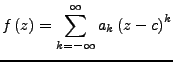
![]() ,
und
,
und