




Next: Kombinatorik
Up: Mengen, natürliche Zahlen, Induktion
Previous: Relationen
Contents
Index
Subsections
Eine Relation
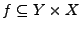 heißt Abbildung
oder Funktion falls es zu jedem
heißt Abbildung
oder Funktion falls es zu jedem 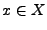 genau
ein
genau
ein 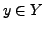 gibt mit
gibt mit
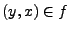 . Schreibe
. Schreibe
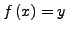 falls
falls 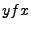 . Schreibe dafür kurz
. Schreibe dafür kurz
- Ist
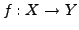 eine Abbildung, und ist
eine Abbildung, und ist
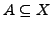 , so
ist
, so
ist
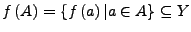 das
das  -Bild von
-Bild von 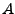 . Ist
. Ist
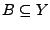 , so ist
, so ist
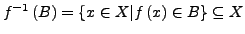 das
das  -Urbild von
-Urbild von 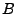 .
.
- Sei
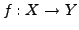 eine Abbildung. Für
eine Abbildung. Für
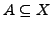 definiere
definiere
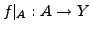 mit
mit
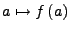 die Einschränkung
von
die Einschränkung
von  auf
auf  .
.
- Es gilt für
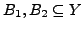
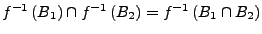
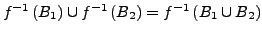
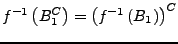
Familie
Eine Famile  ist eine Funktion die
ist eine Funktion die
 ist dabei ein Element aus der Indexmenge, die alle möglichen
ist dabei ein Element aus der Indexmenge, die alle möglichen
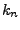 sozusagen durchindiziert.
sozusagen durchindiziert.
Komposition
Sind
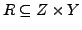 und
und
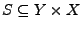 Relationen,
setze
Relationen,
setze
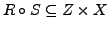 durch
durch
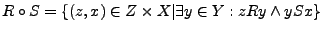 .
.
Speziell: sind
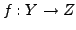 und
und
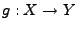 Abbildungen,
so ist
Abbildungen,
so ist 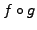 die Abbildung
die Abbildung
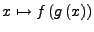 ,
lies ``
,
lies `` nach
nach 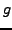 ''.
''.
- Kompositionen sind assoziativ, d.h. es muss nicht geklammert werden.
Eine Abbildung
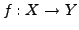 heißt:
heißt:
- surjektiv
- falls es zu jedem
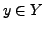 ein
ein 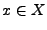 mit
mit
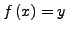 gibt
gibt
- injektiv
- falls
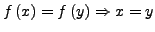 bzw.
bzw.
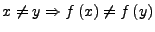
-
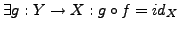
- Verknüpfung von injektiven Funktionen ist wieder injektiv
- bijektiv
- falls sie surjektiv und injektiv ist,
d.h. falls es zu jedem
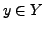 genau ein
genau ein 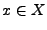 gibt mit
gibt mit
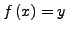





Next: Kombinatorik
Up: Mengen, natürliche Zahlen, Induktion
Previous: Relationen
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]() heißt Abbildung
oder Funktion falls es zu jedem
heißt Abbildung
oder Funktion falls es zu jedem ![]() genau
ein
genau
ein ![]() gibt mit
gibt mit
![]() . Schreibe
. Schreibe
![]() falls
falls ![]() . Schreibe dafür kurz
. Schreibe dafür kurz
![]() ist eine Funktion die
ist eine Funktion die
![]() und
und
![]() Relationen,
setze
Relationen,
setze
![]() durch
durch
![]() .
.
![]() und
und
![]() Abbildungen,
so ist
Abbildungen,
so ist ![]() die Abbildung
die Abbildung
![]() ,
lies ``
,
lies ``![]() nach
nach ![]() ''.
''.
![]() heißt:
heißt: