Lösungsverfahren für LGDL 1. Ordnung

Trennung der Variablen

Lösungsweg für einige einfache Typen von Differentialgleichungen 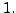$1.$ Ordnung

• schreibe 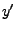$y'$ in der Form $\frac{dy}{dx}$
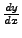
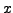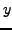• fasse $x$ und $y$ als ``unabhängige Variablen'' auf
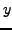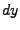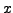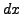• $y$ und $dy$ auf eine Seite, $x$ und $dx$ auf die andere
• Integriere auf beiden Seiten
• Löse nach 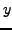$y$ auf

Lösen von inhomogenen Gleichungen

Die Lösung einer LDGL 1. Ordnung setzt sich zusammen aus einer allg. Lösung der homogenen Gleichung und einer speziellen Lösung der inhomogenen Gleichung.

1. Allg. Lösung der homogenen LDGL
   $y'+f\left(x\right)y=0$
   $y_{H}\left(x\right)=y_{0}e^{-\int_{x_{0}}^{x}d\tilde{x}f\left(\tilde{x}\right)}$
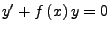
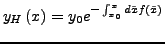
2. Ansatz
   $y_{I}\left(x\right)=\alpha\left(x\right)e^{-\int_{x_{0}}^{x}d\tilde{x}f\left(\tilde{x}\right)}$
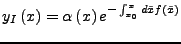
   Randbedingung $\alpha\left(x_{0}\right)=y_{0}$
   $A=\int_{x_{0}}^{x}d\tilde{x}f\left(\tilde{x}\right)$
   $y_{I}=\alpha\left(x\right)e^{-A\left(x\right)}$
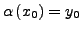
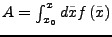
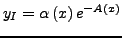
3. Bestimmung von $\alpha\left(x\right)$
   $y_{I}'\left(x\right)=\alpha'\left(x\right)e^{-A\left(x\right)}-\alpha\left(x\right)f\left(x\right)e^{-A\left(x\right)}$
   $\alpha'\left(x\right)=g\left(x\right)e^{A\left(x\right)}$
   $\alpha\left(x\right)=\alpha\left(x_{0}\right)+\int_{x_{0}}^{x}d\tilde{x}g\left(\tilde{x}\right)e^{A\left(x\right)}$
   $y\left(x\right)=y_{0}e^{-A\left(x\right)}+\int_{x_{0}}^{x}d\tilde{x}g\left(\tilde{x}\right)e^{A\left(\tilde{x}\right)-A\left(x\right)}$

Vereinfachen durch Substitution

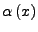
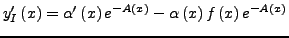
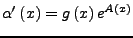
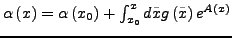
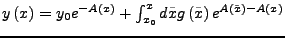
Durch geschicktes wählen von 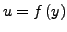$u=f\left(y\right)$ lassen sich inhomogene Differentialgleichungen oder komplizierte homogene DGL manchmal auf eine einfache Form zurückführen.