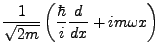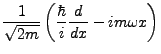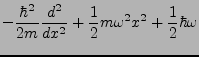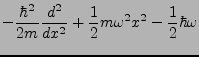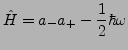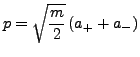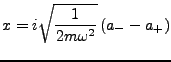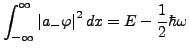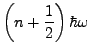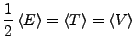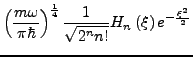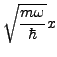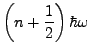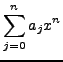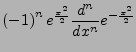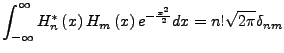Next: Das ``freie'' Teilchen
Up: Zeitunabhängige Schrödinger Gl.
Previous: Kastenpotential mit unendlich hohen
Contents
Index
Subsections
- In der Umgebung eines lokalen Extremums lässt sich jede Funktion Näherungsweise
als Parabel auffassen.
- Harmonische Oszillatoren in klassischer Mechanik
- Definiere
- Operatoridentitäten
- Hamilton Operator
- Impuls
- Ort
- Kommutator
-
![$ \left[A,B\right]=AB-BA$](img127.png)
- Lösungen
- falls
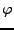 Lösung der Schrödinger Gleichung für
Energie
Lösung der Schrödinger Gleichung für
Energie 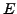 , dann ist
, dann ist
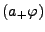 Lösung für die
Energie
Lösung für die
Energie
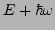 und
und
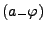 Lösung für
die Energie
Lösung für
die Energie
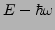 .
.
- Normierung
- falls
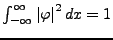 gilt
gilt
- Lösungen
-
- Iterative
- Lösung
- die Phase von
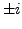 ist eigentlich irrelevant, ist aber so in der
Konvention
ist eigentlich irrelevant, ist aber so in der
Konvention
-
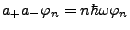
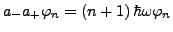
-
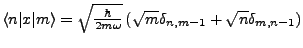
- Viralsatz
- besagt (nur beim harmonischen Oszillator)
- Lösung
-
- Hermite Polynome
-
-
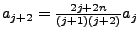
-
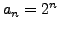
- Es kommen je nachdem ob
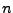 gerade oder ungerade ist nur gerade oder
ungerade Potenzen in
gerade oder ungerade ist nur gerade oder
ungerade Potenzen in
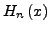 vor.
vor.
- Bilden ein Orthogonalsystem
- Lösen die DGL mit
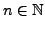





Next: Das ``freie'' Teilchen
Up: Zeitunabhängige Schrödinger Gl.
Previous: Kastenpotential mit unendlich hohen
Contents
Index
Marco Möller 21:20:46 15.11.2006
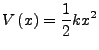
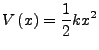
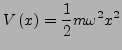
![$\displaystyle \frac{1}{2m}\left[\left(\frac{\hbar}{i}\frac{d}{dx}\right)^{2}+\left(m\omega x\right)^{2}\right]\varphi\left(x\right)=E\varphi\left(x\right)$](img114.png)