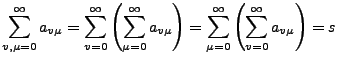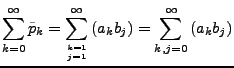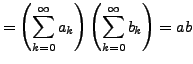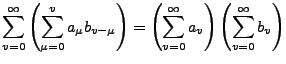Next: Konvergenzkriterien II.168
Up: Reihen II.22
Previous: Konvergenz II.22
Contents
Index
Subsections
absolut / bedingt konvergent
II.163
Die Reihe
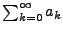 heißt absolut konvergent, falls
die Reihe
heißt absolut konvergent, falls
die Reihe
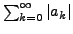 konvergiert, bedingt
konvergent, falls zwar
konvergiert, bedingt
konvergent, falls zwar
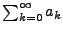 konvergiert,
konvergiert,
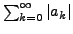 aber divergiert.
aber divergiert.
- Wenn eine Reihe
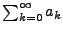 absolut konvergiert, dann
konvergiert sie auch bedingt.
absolut konvergiert, dann
konvergiert sie auch bedingt.
- Wenn eine Reihe
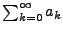 divergiert, dann divergiert
auch
divergiert, dann divergiert
auch
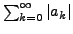 .
.
- Die Summe (
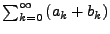 ) zweier
absolut konvergenter Reihen (
) zweier
absolut konvergenter Reihen (
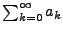 ,
,
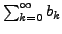 )
ist die auch absolut konvergent.
)
ist die auch absolut konvergent.
Doppelreihe II.167
Durch
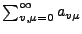 wird eine Doppelreihe gegeben.
wird eine Doppelreihe gegeben.
Umordnung II.164
Sei
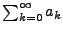 eine Reihe und
eine Reihe und
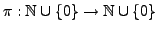 eine bijektive Abbildung. Dann heißt die Reihe
eine bijektive Abbildung. Dann heißt die Reihe
eine Umordnung der Ausgangsreihe.
- Jede Umordnung einer absolut konvergenten Reihe ist ebenfalls (gegen
den gleichen Wert) konvergent.
- Sei
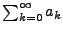 bedingt konvergent. Dann gibt es zu
jedem
bedingt konvergent. Dann gibt es zu
jedem
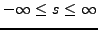 eine Umordnung sie bedingt gegen
eine Umordnung sie bedingt gegen
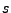 konvergiert:
konvergiert:
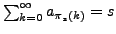
Großer Umordnungssatz II.167
Ordnet man die Doppelreihe in beliebiger Reihenfolge zu einer einfachen
Reihe an, so entsteht eine stets mit der gleichen Summe 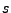 absolut
konvergente Reihe. Alle Zeilensummen
absolut
konvergente Reihe. Alle Zeilensummen
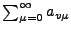 sowie alle Spaltensummen
sowie alle Spaltensummen
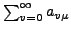 sind absolut konvergent. Die Reihe der Spaltensummen bzw. Reihensummen
konvergiert absolut gegen
sind absolut konvergent. Die Reihe der Spaltensummen bzw. Reihensummen
konvergiert absolut gegen 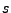 :
:
- gilt sinngemäß auch für Mehrfachreihen
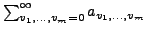
Produkt von Reihen II.165
Wenn zwei Reihen absolut konvergieren, dann konvergiert die Reihe
der Produkte (bei beliebiger Anordnung) ebenfalls absolut, und es
gilt:
Cauchy-Produkt II.166
Das Cauchy-Produkt ist absolut konvergent:





Next: Konvergenzkriterien II.168
Up: Reihen II.22
Previous: Konvergenz II.22
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() heißt absolut konvergent, falls
die Reihe
heißt absolut konvergent, falls
die Reihe
![]() konvergiert, bedingt
konvergent, falls zwar
konvergiert, bedingt
konvergent, falls zwar
![]() konvergiert,
konvergiert,
![]() aber divergiert.
aber divergiert.
![]() wird eine Doppelreihe gegeben.
wird eine Doppelreihe gegeben.
![]() eine Reihe und
eine Reihe und
![]() eine bijektive Abbildung. Dann heißt die Reihe
eine bijektive Abbildung. Dann heißt die Reihe
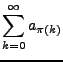
![]() absolut
konvergente Reihe. Alle Zeilensummen
absolut
konvergente Reihe. Alle Zeilensummen
![]() sowie alle Spaltensummen
sowie alle Spaltensummen
![]() sind absolut konvergent. Die Reihe der Spaltensummen bzw. Reihensummen
konvergiert absolut gegen
sind absolut konvergent. Die Reihe der Spaltensummen bzw. Reihensummen
konvergiert absolut gegen ![]() :
: