Next: Besondere Reihen
Up: Reihen II.22
Previous: absolut / bedingt konvergent
Contents
Index
Subsections
Konvergenzkriterien
II.168
Majoranten- oder Vergleichskriterium
II.168
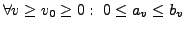 .
.
Wenn die Reihe
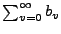 konvergiert, dann konvergiert
auch die Reihe
konvergiert, dann konvergiert
auch die Reihe
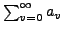 , und es gilt:
, und es gilt:
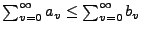 .
.
Wenn die Reihe
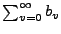 divergiert, dann divergiert
auch die Reihe
divergiert, dann divergiert
auch die Reihe
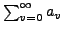 .
.
Quotientenkriterium II.169
Sei
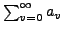 eine Reihe mit
eine Reihe mit 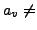 für alle
für alle
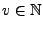 und
und
Dann gilt:
- Ist
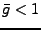 , so konvergiert die Reihe
, so konvergiert die Reihe
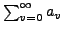 absolut.
absolut.
- Ist
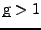 , so divergiert die Reihe
, so divergiert die Reihe
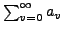 .
.
- Für jeweils
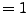 gibt das Kriterium keinen Aufschluss.
gibt das Kriterium keinen Aufschluss.
- siehe Wurzelkriterum (ist stärker als Quotientenkriterium)
Wurzelkriterium II.171
Sei
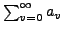 eine Reihe mit
eine Reihe mit
Leibnizsches Kriterium II.174
Sei
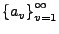 eine Nullfolge
mit
eine Nullfolge
mit
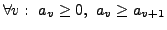 .
.
Dann ist die Reihe
konvergent. Für die n-te Teilsumme gilt die Abschätzung:
Integralkriterium II.175
Sei
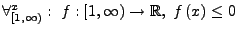 monoton fallend, und die Folge
monoton fallend, und die Folge
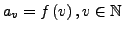 eine Nullfolge. Dann gilt:
eine Nullfolge. Dann gilt:





Next: Besondere Reihen
Up: Reihen II.22
Previous: absolut / bedingt konvergent
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() .
.
![]() konvergiert, dann konvergiert
auch die Reihe
konvergiert, dann konvergiert
auch die Reihe
![]() , und es gilt:
, und es gilt:
![]() .
.
![]() divergiert, dann divergiert
auch die Reihe
divergiert, dann divergiert
auch die Reihe
![]() .
.
![]() eine Reihe mit
eine Reihe mit ![]() für alle
für alle
![]() und
und
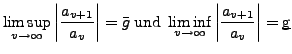
![]() eine Reihe mit
eine Reihe mit
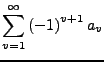
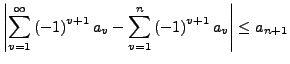
![]() monoton fallend, und die Folge
monoton fallend, und die Folge
![]() eine Nullfolge. Dann gilt:
eine Nullfolge. Dann gilt: