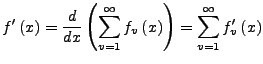Die Folge
![]() von stetigen Funktionen
konvergiere gleichmäßig gegen die Grenzfunktion
von stetigen Funktionen
konvergiere gleichmäßig gegen die Grenzfunktion ![]() . Dann gilt
. Dann gilt
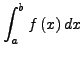 |
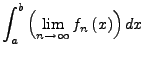 |
||
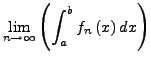 |
Die Folge von stetig differenzierbaren Funktionen
![]() konvergiere in
konvergiere in
![]() punktweise gegen
punktweise gegen ![]() . Die Folge
der Ableitungen
. Die Folge
der Ableitungen
![]() konvergiere
gleichmäßig in
konvergiere
gleichmäßig in
![]() . Dann ist
. Dann ist ![]() stetig diffbar,
und
stetig diffbar,
und
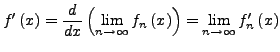
Sei
![]() stetig auf
stetig auf
![]() .
Die Reihe
.
Die Reihe
![]() konvergiere gleichmäßig auf
konvergiere gleichmäßig auf
![]() . Dann ist die Grenzwertfunktion
. Dann ist die Grenzwertfunktion
![]() stetig in
stetig in
![]() und
und
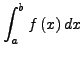 |
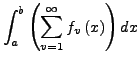 |
||
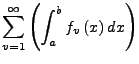 |
Sei
![]() stetig differenzierbar auf
stetig differenzierbar auf
![]() . Die Reihe
. Die Reihe
![]() konvergiere punktweise gegen
konvergiere punktweise gegen ![]() , und
, und
![]() konvergiere gleichmäßig auf
konvergiere gleichmäßig auf
![]() . Dann ist
. Dann ist
![]() stetig
differenzierbar und
stetig
differenzierbar und