




Next: Grenzwert von Funktionen
Up: Funktionen I.116
Previous: Stetige Funktionen II.38
Contents
Index
Subsections
Seien
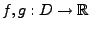 stetig in
stetig in
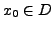 . Dann
sind auch folgende Funktionen stetig:
. Dann
sind auch folgende Funktionen stetig:
Verkettung II.42
Sei
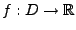 stetig in
stetig in
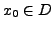 ,
,
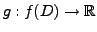 stetig in
stetig in
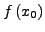 . Dann gilt:
. Dann gilt:
Verkettung
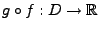 ist stetig.
ist stetig.
bzw.
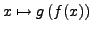 stetig in
stetig in 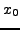
Umkehrfunktion II.43
Sei
![$ f:\left[a,b\right]\rightarrow\mathbb{R}$](img345.png) eine streng monotone,
in
eine streng monotone,
in
![$ x_{0}\in\left[a,b\right]$](img442.png) stetige Funktion. Dann ist die Umkehrfunktion
stetige Funktion. Dann ist die Umkehrfunktion
![$ f^{-1}:f\left(\left[a,b\right]\right)\rightarrow\mathbb{R}$](img443.png) in
in
![$ f\left(x_{0}\right)\in f\left(\left[a,b\right]\right)$](img444.png) stetig.
stetig.
- Entspricht einer Spiegelung der Funktion an der Geraden
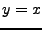
-
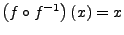
- Nur !!! bei stetigen, streng monotonen Funktionen möglich. Anderenfalls
Definitionsbereich passend einschränken.
Min-/Maximum II.43
Eine Funktion hat ein (absolutes) Minimum bzw. Maximum 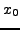 , wenn
, wenn
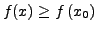 bzw.
bzw.
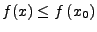 .
.
Bei einem beschränkten Wertebereich muss eine stetige Funktion ein
absolutes Minimum und ein absolutes Maximum besitzen.
Dies ist relativ, falls dies nur in einer Umgebung um 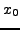 gilt.
gilt.
Zwischenwertsatz II.44
Bei einer stetigen, beschränkten Funktion wird jeder Wert zwischen
dem Minimum und dem Maximum als Funktionswert angenommen.
gerade / ungerade
Funktionen





Next: Grenzwert von Funktionen
Up: Funktionen I.116
Previous: Stetige Funktionen II.38
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() stetig in
stetig in
![]() . Dann
sind auch folgende Funktionen stetig:
. Dann
sind auch folgende Funktionen stetig:
![]() stetig in
stetig in
![]() ,
,
![]() stetig in
stetig in
![]() . Dann gilt:
. Dann gilt:
![]() ist stetig.
ist stetig.
![]() stetig in
stetig in ![]()
![]() eine streng monotone,
in
eine streng monotone,
in
![]() stetige Funktion. Dann ist die Umkehrfunktion
stetige Funktion. Dann ist die Umkehrfunktion
![]() in
in
![]() stetig.
stetig.
![]() , wenn
, wenn
![]() bzw.
bzw.
![]() .
.
![]() gilt.
gilt.