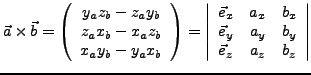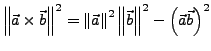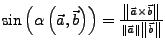Das vektorielle Produkt
![]() ordnet zwei
Vektoren
ordnet zwei
Vektoren ![]() und
und ![]() einen dritten Vektor
einen dritten Vektor ![]() zu. Man stelle sich vor,
zu. Man stelle sich vor, ![]() und
und ![]() spannen im Raum
eine Fläche (Parallelogramm) auf.
spannen im Raum
eine Fläche (Parallelogramm) auf. ![]() wird auf dieser Fläche
senkrecht stehen, und als Länge, den Betrag des Flächeninhalts des
Parallelogramms haben. Die genaue Richtung lässt sich mit der 3-Fingerregel
überlegen. Daumen =
wird auf dieser Fläche
senkrecht stehen, und als Länge, den Betrag des Flächeninhalts des
Parallelogramms haben. Die genaue Richtung lässt sich mit der 3-Fingerregel
überlegen. Daumen = ![]() ; Zeigefinger (ausgestreckt) =
; Zeigefinger (ausgestreckt) = ![]() ;
Mittelfinger (90^&cir#circ; angewinkelt) =
;
Mittelfinger (90^&cir#circ; angewinkelt) = ![]()