




Next: Lineare Abbildungen I.183
Up: Vektorräume I.159
Previous: Koordinaten I.171
Contents
Index
Subsections
Der unitäre Vektorraum
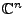 I.177
I.177
Übertragen des Skalarproduktes und des Betrages auf den Vektorraum
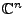 .
.
Skalare Produkt /
Betrag I.178
Es gelten die selben Regeln wie für Vektoren aus
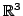 (siehe sub:skalare-Produkt-R3) mit folgenden Ausnahmen bzw.
Ergänzungen:
(siehe sub:skalare-Produkt-R3) mit folgenden Ausnahmen bzw.
Ergänzungen:
-
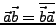
-
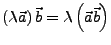
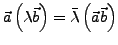
- Die Vektoren
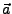 und
und 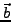 heißen orthogonal
(senkrecht) zueinander
heißen orthogonal
(senkrecht) zueinander
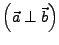 ,
wenn
,
wenn
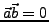
- Vektoren der Länge 1
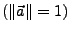 heißen Einheitsvektoren.
heißen Einheitsvektoren.
Orthogonalsystem
/ Orthonormalsystem (Basis) I.180
Eine Menge von Vektoren
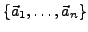 ,
die den Nullvektor nicht enthält und mit
,
die den Nullvektor nicht enthält und mit
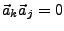 für
für 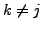 heißt Orthogonalsystem (alle Vektoren sind senkrecht
zueinander).
heißt Orthogonalsystem (alle Vektoren sind senkrecht
zueinander).
Sind zudem alle
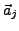 normiert (Länge 1) so heißen sie Orthonormalsystem.
normiert (Länge 1) so heißen sie Orthonormalsystem.
- Die Vektoren eines Orthonormalsystems sind linear unabhängig
- Bilden die Vektoren eine Basis, so spricht man von einer Orthogonalbasis
bzw. Orthonormalbasis.
- Die Kanonische Basis ist eine Orthonormalbasis (siehe sub:Kanonische-Basis).
Existenz einer Orthonormalbasis
I.181
Sei
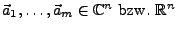 eine linear unabhängige Menge von Vektoren. Dann gibt es ein Orthonormalsystem
eine linear unabhängige Menge von Vektoren. Dann gibt es ein Orthonormalsystem
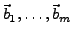 mit
mit
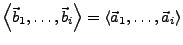 für alle
für alle
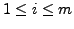 .
.
Gram-Schmidtsches-Orthonormalisierungsverfahren
I.182
Auch unter dem Namen Hilbert-Schmidtsches-Orthonormalisierungsverfahren
bekannt. Konventionen wie bei 18.4.3.
-
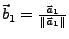
- Für alle
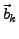 mit
mit
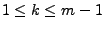
-
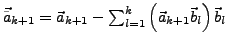
-
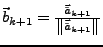
- Alle
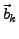 auf Länge (=1) und orthogonalität (Skalarprodukt
= 0) testen
auf Länge (=1) und orthogonalität (Skalarprodukt
= 0) testen
- Brüche und Große Zahlen aus Vektoren ausklammern, so das in den Vektoren
nur ganze, möglichst kleine Zahlen enthalten sind.
- Um aus
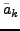
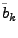 zu erstellen, können die
ausgeklammerten Werte vor
zu erstellen, können die
ausgeklammerten Werte vor
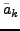 weggelassen werde, da diese
sich durchs Renormieren ohnehin herauskürzen würden.
weggelassen werde, da diese
sich durchs Renormieren ohnehin herauskürzen würden.
Geometrisch wird der die Richtung des 1. Vektors übernommen, und von
allen weiteren Vektoren deren Komponenten in Richtung von bereits
erzeugten Basis-Vektoren abgezogen, so das nur deren neuer Richtungsanteil
übrig bleibt, welcher letztendlich dann als Richtung für den zusätzlichen
Basis-Vektor genommen wird.





Next: Lineare Abbildungen I.183
Up: Vektorräume I.159
Previous: Koordinaten I.171
Contents
Index
Marco Möller 17:42:11 24.10.2005
![]() .
.
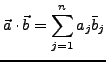
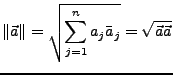
![]() (siehe sub:skalare-Produkt-R3) mit folgenden Ausnahmen bzw.
Ergänzungen:
(siehe sub:skalare-Produkt-R3) mit folgenden Ausnahmen bzw.
Ergänzungen:
![]() ,
die den Nullvektor nicht enthält und mit
,
die den Nullvektor nicht enthält und mit
![]() für
für ![]() heißt Orthogonalsystem (alle Vektoren sind senkrecht
zueinander).
heißt Orthogonalsystem (alle Vektoren sind senkrecht
zueinander).
![]() normiert (Länge 1) so heißen sie Orthonormalsystem.
normiert (Länge 1) so heißen sie Orthonormalsystem.
![]() eine linear unabhängige Menge von Vektoren. Dann gibt es ein Orthonormalsystem
eine linear unabhängige Menge von Vektoren. Dann gibt es ein Orthonormalsystem
![]() mit
mit
![]() für alle
für alle
![]() .
.