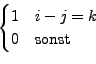Next: Lineares Vektorfeld
Up: Vektorfelder und Flüsse
Previous: 1-Parametergruppe von Abbildungen
Contents
Index
Subsections
Exponentialfunktion
Sei 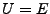 Banachraum z.B.
Banachraum z.B.
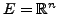
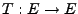 linear und stetig (
linear und stetig (
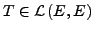 ).
).
Ist 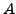 eine Blockdiagonalmatrix,
d.h.
eine Blockdiagonalmatrix,
d.h.
mit
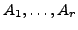 ebenfalls Matritzen. Dann gilt
ebenfalls Matritzen. Dann gilt
- Dies ist für Diagonalmatrizen bereits eine geschlossene Lösungsformel
- gilt ebenso für komplexe Matritzen
Ist
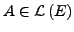 und ist
und ist
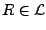 invertierbar
(d.h.
invertierbar
(d.h.
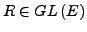 ), so gilt
), so gilt
- gilt ebenso für komplexe Matritzen
Eine komplexe 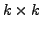 -Matrix der Form
-Matrix der Form
für
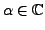 , heißt Jordan-Block
der Größe
, heißt Jordan-Block
der Größe 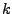 zum Eigenwert
zum Eigenwert 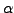 .
.
Ist
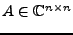 , so gibt es
, so gibt es
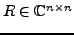 ,
,
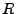 invertierbar, so dass gilt
invertierbar, so dass gilt
ist Blockdiagonal und
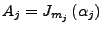 ist
Jordanblock.
ist
Jordanblock. 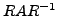 nennt sich die Jordan-Normalform
von
nennt sich die Jordan-Normalform
von 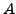 .
.
Eine Matrix
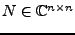 heißt nilpotent,
falls
heißt nilpotent,
falls 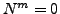 gilt für ein
gilt für ein
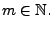
Ist
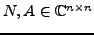 ,
, 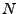 nilpotent mit
nilpotent mit 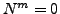 und gilt
und gilt 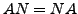 , so gilt
, so gilt
-
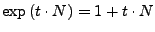 +
+
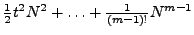
-
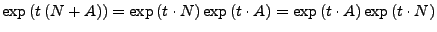
Setze
Hiermit lässt sich ein Jordan Block schreiben als
Hiermit gilt nun





Next: Lineares Vektorfeld
Up: Vektorfelder und Flüsse
Previous: 1-Parametergruppe von Abbildungen
Contents
Index
Marco Möller 12:27:24 18.02.2006
![]() Banachraum z.B.
Banachraum z.B.
![]()
![]() linear und stetig (
linear und stetig (
![]() ).
).
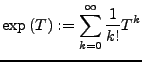
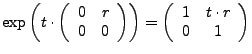
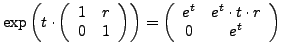
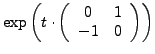
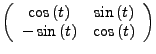
![]() eine Blockdiagonalmatrix,
d.h.
eine Blockdiagonalmatrix,
d.h.

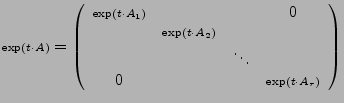
![]() und ist
und ist
![]() invertierbar
(d.h.
invertierbar
(d.h.
![]() ), so gilt
), so gilt
![]() -Matrix der Form
-Matrix der Form
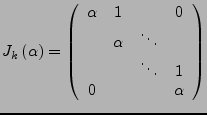
![]() , so gibt es
, so gibt es
![]() ,
,
![]() invertierbar, so dass gilt
invertierbar, so dass gilt
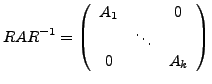
![]() heißt nilpotent,
falls
heißt nilpotent,
falls ![]() gilt für ein
gilt für ein
![]()
![]() ,
, ![]() nilpotent mit
nilpotent mit ![]() und gilt
und gilt ![]() , so gilt
, so gilt