




Next: Jordansche Normalform
Up: Diagonalisierung normaler Matrizen
Previous: Normale Matrizen und Eigenwerte
Contents
Index
Subsections
Sei
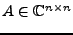 . Äquivalent sind:
. Äquivalent sind:
 ist normal
ist normal
-
 besitzt Orthonormalbasis aus Eigenvektoren von
besitzt Orthonormalbasis aus Eigenvektoren von 
- Es existiert
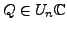 , so dass
, so dass 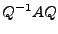 Diagonalmatrix
Diagonalmatrix
Sei
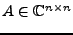 . Äquivalent sind:
. Äquivalent sind:
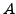 ist hermitesch
ist hermitesch
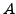 normal & alle Eigenwerte reell
normal & alle Eigenwerte reell
- Es existiert
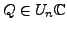 , so dass
, so dass 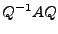 eine reelle
Diagonalmatrix ist
eine reelle
Diagonalmatrix ist
Sei
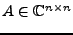 . Äquivalent sind:
. Äquivalent sind:
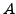 symmetrisch
symmetrisch
-
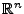 besitzt Orthonormalbasis aus Eigenvektoren von
besitzt Orthonormalbasis aus Eigenvektoren von 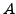
- Es existiert
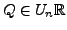 , so dass
, so dass 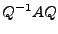 (reelle)
Diagonalmatrix
(reelle)
Diagonalmatrix
Sei
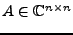 . Äquivalent sind:
. Äquivalent sind:
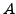 unitär, d.h.
unitär, d.h.
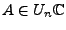
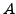 normal & alle Eigenwerte haben Betrag
normal & alle Eigenwerte haben Betrag 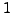
- Es existiert
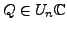 , so dass
, so dass 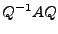 Diagonalmatrix
mit Elementen vom Betrag
Diagonalmatrix
mit Elementen vom Betrag 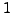 .
.
Marco Möller 20:09:10 02.12.2005
![]() . Äquivalent sind:
. Äquivalent sind:
![]() . Äquivalent sind:
. Äquivalent sind:
![]() . Äquivalent sind:
. Äquivalent sind:
![]() . Äquivalent sind:
. Äquivalent sind: