




Next: Grundlagen der numerischen Simulation
Up: Zeitkontinuierliche Simulierung und Simulation
Previous: Beschreibung zeitkontinuierlicher Systeme
Contents
Index
Subsections
Modellanalyse
Lösbarkeit
- Lösungstrajektorie
- Man zeichne in ein
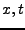 Diagramm (
Diagramm (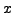 kann
Dimension größer
kann
Dimension größer 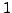 haben, dann dafür mehrere Achsen verwenden)
in jeden Punkt einen Pfeil mit der Steigung
haben, dann dafür mehrere Achsen verwenden)
in jeden Punkt einen Pfeil mit der Steigung
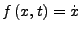 ein (Richtungsfeld). Wenn man nun im
Punkt
ein (Richtungsfeld). Wenn man nun im
Punkt
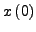 (
(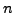 Integrationskonstanten) startet und
immer den Pfeilrichtungen folgt, erhält mein eine Lösungstrajektorie.
Integrationskonstanten) startet und
immer den Pfeilrichtungen folgt, erhält mein eine Lösungstrajektorie.
- eindeutige Lösung
-
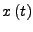 mit
mit 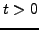 für ein autonomes
DGL-System
für ein autonomes
DGL-System 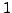 ter Ordnung existiert falls für alle (zulässigen)
ter Ordnung existiert falls für alle (zulässigen)
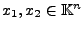 die folgende Lipschitzbedingung erfüllt ist. Es exisitert ein
die folgende Lipschitzbedingung erfüllt ist. Es exisitert ein
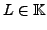 so dass für alle (zulässigen)
so dass für alle (zulässigen)
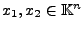 gilt
mit einer belibigen Norm
gilt
mit einer belibigen Norm
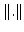 .
.
Gleichgewichtslösung
Außer der Existenz einer (eindeutigen) Lösung von
ist die Existenz eines stationären Zustandes
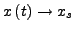 für
für
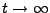 für konstantes
für konstantes
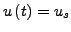 von Interesse.
von Interesse.
- Notwendig
-
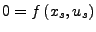
- Lineares System
-
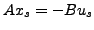 eindeutig Lösbar mit
eindeutig Lösbar mit
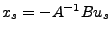 wenn
wenn
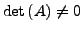
- Lösbar sobald
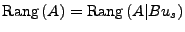
- Nichtlineares System
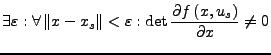
- ist zudem notwendig das die Determinante der
Jakobimatrix im Lösungsumfeld
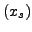 nicht 0 ist.
nicht 0 ist.
- Es kann keine, eine, mehrere, unendlich viele oder keine Lösung geben.
Jacobi-Matrix
Vorwärtsdifferentenquotient
- Besetztheisstruktur
- einer Jacobi-Matrix
gibt wieder, in welchen Stellen der Matrix von 0 verschiedene Werte
stehen.
- Dies gibt die Kopplungen der DGL wieder
- sehr große Systeme können nur durch Ausnutzung der (hoffentlich dünnen)
Besetztheitsstruktur der Jakobimatrix effizient numerisch simuliert
werden.
- Schrittweise Aufdatierung
- (``Updates'')
einer Approximation der Jacobi-Matrix (sogenanntes ``Quasi Newton
Verfahren'')
- im Allgemeinen: Rang
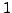 Verfahren z.B. nach Broyden:
Verfahren z.B. nach Broyden:
Approximation der Jacobimatrix
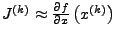 durch schrittweise Aufaddierung einer
durch schrittweise Aufaddierung einer 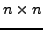 Matrix vom Rang
Matrix vom Rang
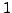 (rank
(rank 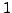 update)
update)
-
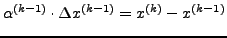
- Bei symmetrischer Jacobi-Matrix: Rang 2-Verfahren
- Symbolisches Differenzieren
- durch
systematisches Anwenden von Ketten-, Produkt etc. Regeln
- z.B. mit Maple, Mathematica, Macsyma
- Vorteil: kein Approximierungsfehler, nur Rundungsfehler
- Nachteil: liefert lange, unübersichtliche Formeln; hoher Berechnungsaufwand
- Automatisches Differenzieren
- sind
spezielle Algorithmen zur Transformation eines C-, Fortran oder Matlab-
Programms von
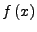 in Programm zur Auswertung der Jacobi-Matrix
in Programm zur Auswertung der Jacobi-Matrix
- Vorteil: kein Approximatinsfehler, nur Rundungsfehler
- Schwierigkeiten u.a. bei Fallunterscheidungen (if-then-else)
Linearisierung um die Ruhelage
-
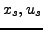 sind Koordinaten der jeweiligen Ruhelage um die linearisiert
wird
sind Koordinaten der jeweiligen Ruhelage um die linearisiert
wird
- Fällt ein Ruhezustand mit einer Sprung- oder Knickstelle (oder anderen
Ausnahmestelle) zusammen, so kann man um ihn nicht linearisieren (und
auch nicht in einer ``engeren'' Umgebung).
- Es lässt sich auch um eine Referenztrajektorie linearisiern. Formeln
sehen genauso aus wie hier. Interpretierbar als Linearisierung um
zeitveränderliche Ruhelage
Lösen einer linearisierten (linearen)
DGL
- Gegeben
-
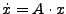
- Lösungsansatz
-
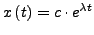
- Zwischentherm
-
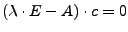
- Eigenwerte von
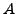 als Lösungen für
als Lösungen für 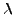 bestimmen.
bestimmen. 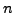 komplexe
Lösungen für folgende Gleichung:
komplexe
Lösungen für folgende Gleichung:
- Lösung
-
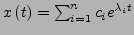
Stabilität
Für den Fall das 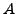 eine rein reelle Matrix war gilt:
eine rein reelle Matrix war gilt:
- aperiodische Dämpfung
- wenn alle Eigenwerte reell und negativ sind
- aperiodisch ungedämpft
- wenn alle Eigenwerte reell und mind. einer
positiv ist
- gedämpfte Oszilation
- wenn alle Realanteile der Eigenwerte negativ
sind und komplexe Eigenwerte immer konjungiert nocheinmal auftauchen.
- ungedämpfte Oszillation
- wenn mindestens ein
Realanteil eines Eigenwertes positiv ist und komplexe Eigenwerte immer
konjungiert nocheinmal auftauchen.
- instabil
- bedeutet das bei einer begrenzen Eingabe eine theoretisch
unbegrenzte Ausgabe erfolgen kann.
Zeitcharakteristik
- Zeitcharakteristika
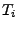
- sind für aperiodische Vorgänge die Dauer, bis sich der Wert um den
Faktor
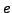 (bzw.
(bzw.
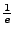 ) verändet hat
) verändet hat
- sind für periodische Vorgänge die Periodendauer
- können mit Hilfe der Eigenwerte
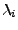 bestimmt werden
bestimmt werden
- reeller EW
-
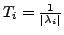
- imaginärer EW
-
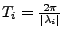
- Simulationsdauer
- für nichtlineares System
(Faustregel)
- stabiles System:
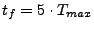
- instabiles System bis z.B. ein gewünschter Wert über-/unterschritten
wurde
- Diskretisierungsschrittweite
-
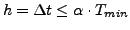
- mit
![$ \alpha\in\left[\frac{1}{20},\frac{1}{5}\right]$](img183.png)
Steife DGL
- Definition
- Eine DGL wird steif genannt wenn sie sehr unterschiedliche
Zeitcharakteristika enthält
- Steifheitsmaß
-
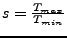
- numerische Lösung benötigt Rechenzeit Proportional zu
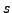
- Integration
- von steifen DGLn am besten mit implizieten Verfahren
Die rechte Seite 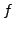 der Differentialgleichung
der Differentialgleichung
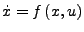 (oder eine ihrer Ableitungen) kann unstetig
sein, z.B. wegen
(oder eine ihrer Ableitungen) kann unstetig
sein, z.B. wegen
- unstetiger Steuerung
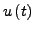 , z.B. Ventil auf/zu
, z.B. Ventil auf/zu
- modellinhärenter Unstetigkeiten (z.B. Kollision von Roboterarm, Abtrennung
einer Raketenbrennstufe)
- Einige numerische Methoden benötigen (mehrfach) stetig ableitbare
rechte Seite. Hier Vorsicht walten lassen bzw. berücksichtigen.
- Verbesserung der numerischen Simulation durch Detektion der Unstetigkeit
und abschnittsweiser Berechnung.





Next: Grundlagen der numerischen Simulation
Up: Zeitkontinuierliche Simulierung und Simulation
Previous: Beschreibung zeitkontinuierlicher Systeme
Contents
Index
Marco Möller 17:20:55 24.10.2005

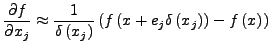
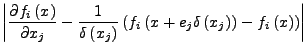
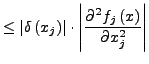
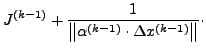
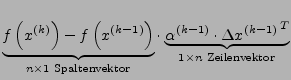
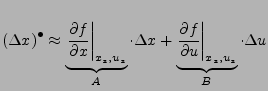
![]() eine rein reelle Matrix war gilt:
eine rein reelle Matrix war gilt:
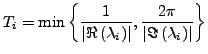
![]() der Differentialgleichung
der Differentialgleichung
![]() (oder eine ihrer Ableitungen) kann unstetig
sein, z.B. wegen
(oder eine ihrer Ableitungen) kann unstetig
sein, z.B. wegen