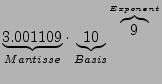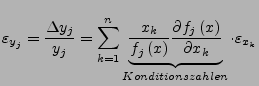Next: Berechnung nichtlinearer Gleichgewichtslösungen
Up: Zeitkontinuierliche Simulierung und Simulation
Previous: Modellanalyse
Contents
Index
Subsections
- Normalisierte Gleitpunktzahl
- Zahl bei dem genau eine Stell vor
dem Komme ungleich 0 ist. Die entsprechende Kommaverschiebung wird
im Exponenten des Faktors untergebracht.
- Basis
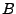 feste Zahl, z.B. 10 (Dezimal) oder 2 (Binär)
feste Zahl, z.B. 10 (Dezimal) oder 2 (Binär)
- bei Basis
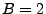 braucht
braucht 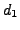 nicht expliziet gespeichert werden,
da es durch die Normalisierung
nicht expliziet gespeichert werden,
da es durch die Normalisierung 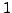 sein muss
sein muss
- Exponent
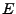 ganze Zahl und beschränkt
ganze Zahl und beschränkt
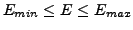
- mehr Bits für den Exponenten ergibt größeren Zahlenbereich
- Ziffern
-
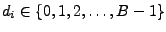
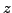 normalisiert wenn
normalisiert wenn
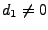
- Mantisse
-
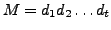
- Länge der Mantisse
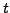 (konstant)
(konstant)
- mehr Bits für die Mantisse ergibt größeren (relative) Genauigkeit
- Es gibt eine größte und eine kleinste darstellbare Zahl
- Auf heutigen Computer ist
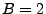 quasi Standard
quasi Standard
- bei Basis
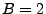 braucht
braucht 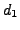 nicht expliziet gespeichert werden,
da es durch die Normalisierung
nicht expliziet gespeichert werden,
da es durch die Normalisierung 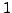 sein muss
sein muss
- Es wird noch ein weiteres Bit für das Vorzeichen gebraucht:
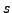
-
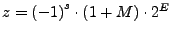
- Einige besondere Belegungen sind reserviert für Unendlich und co:
siehe IEEE 754
- relative Maschienengenauigkeit
- (machine
precision) heißt der Abstand der Zahlen im Intervall
![$ \left[1,2\right]$](img200.png)
- IEEE single precision
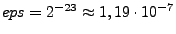
- IEEE double precision
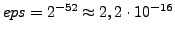
Rundungsfehler
- Rundung
-
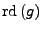 Abbilden einer
Zahl auf die ``am nächsten liegende'' darstellbare Zahl
Abbilden einer
Zahl auf die ``am nächsten liegende'' darstellbare Zahl
- Es gibt unterschiedliche Rundungsarten nach IEEE 754
- R1 immer aufrunden (nach rechts)
- R2 immer abrunden (nach links)
- R3 Runden durch abschneiden (nach Null)
- R4 Runden zur nächsten Zahl (zum Nächsten)
- relative Rundungsfehler
-
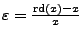
-
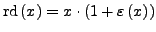
- mit
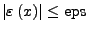
- Für die elementaren arithmetischen Operationen (
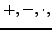 ) gilt
zumindest näherungsweise
) gilt
zumindest näherungsweise
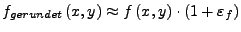 mit
mit
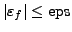
Fortpflanzung von Rundungsfehlern
- Assoziativ- und Distributivgesetz gelten nicht für Gleitpunktarithmetik:
(
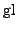 ist Gleitpunktimplementierung der entsprechenden
Funktion)
ist Gleitpunktimplementierung der entsprechenden
Funktion)
- In allen Ausdrücken
sukzessive ersetzen.
Daraus Ermittlung einer Darstellung
mit von Eingangsdaten abhängigen Verstärkungsfaktoren
Kondition
- Gegeben
-
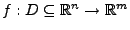 sei
mindestens einmal stetig differenzierbar
sei
mindestens einmal stetig differenzierbar
- absuluter Fehler in
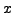
-
- relativer Fehler in
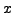
-
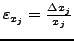
- Konditionszahlen
- (siehe vorherige Formel)
nennt man die Verstärkungsfaktoren des relativen Fehlers in den Eingangsdaten.
- sind diese groß ist das Problem schlecht Konditioniert
- sind diese klein ist das Problem gut Konditioniert
- hängen nicht von der Implementierung der Funktion ab, sondern
nur von deren Eigenschaften
- Multiplikation
-
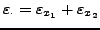
- Division
-
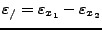
- Addition / Subtraktion
-
- Subtraktion (speziell von gleich großen Zahle) ist extrem schlecht
Konditioniert: Auslöschung
- Wurzel
-
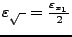
- Numerische Stabilität
- ein
gut Konditioniertes Problem kann bei schlechter Implementierung trotzdem
extreme Fehlerverstärkung haben
- Formel Umformen! Umständlich kann besser als direkt sein! Subtraktionen
vermeiden!





Next: Berechnung nichtlinearer Gleichgewichtslösungen
Up: Zeitkontinuierliche Simulierung und Simulation
Previous: Modellanalyse
Contents
Index
Marco Möller 17:20:55 24.10.2005