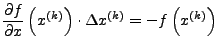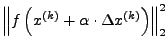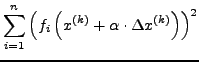Next: Numerische Lösung der nichtlinearen
Up: Zeitkontinuierliche Simulierung und Simulation
Previous: Grundlagen der numerischen Simulation
Contents
Index
Subsections
Newton Verfahren - Basisversion
- Gesucht
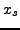 mit
mit
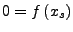
- Start
-
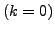 Wahr eines Startvektors
Wahr eines Startvektors
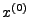
- z.B. aus Kentnissen über das dem Modell zugrundelegene physikalische
Modell
- Ausprobieren
- Herantasten von der bekannten Lösung eines einfacheren Problems (Fortsetzungsmethode)
- Iterationsschritt
-
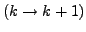
- Berechnung von
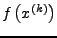
- Berechnung der Jakobimatrix
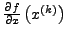
- siehe Abschnitt sub:Jacobi-Matrix
- oder Jakobimatrix durch konstante Matrix, z.B.
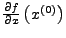 bzw. deren Approximation ersetzen
bzw. deren Approximation ersetzen
- Verfahren nicht mehr quadratisch, höchstens linear konvergent
- Wenn konvergent, dann heufig schneller als ``normales'' Newtonverfahren
- Berechnung der Korrektur (Suchrichtung)
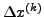 durch lösen des linearen Gleichungssystems
durch lösen des linearen Gleichungssystems
- Berechnung der neuen Näherung
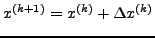
- Terminierungstest
- Falls ``nahe genug'' an der Lösung oder ``kein
Fortschritt'' Stop, ansonsten
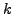 um 1 erhöhen und nächsten
Iterationsschritt.
um 1 erhöhen und nächsten
Iterationsschritt.
- ``Nahe genug'' an der Lösung
- keine nennenswerte Änderung in
- Funktionswerte klein genug
- ``kein Fortschritt'' mehr
- keine nennenswerte Abnahme mehr
- zu viele Iterationsschritte
- Für
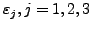 geeignete Toleranzen z.B.
geeignete Toleranzen z.B.
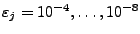
- Es können einige Nullstellen durch andere in Ihrere Umgebung versteck
sein, so dass sie nur gefunden werden wenn der Startwert in einem
(kleinen) Bereich liegt.
Divergenz und Singularitäten
- Singularitäten in der Nähe von Nullstellen können diese ``Verstecken''
- Divergenz obwohl Startwert ``nahe'' an Nullstelle
- Abhilfe
- durch ``kleineren'' Schritt zur Berechnung von
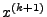





Next: Numerische Lösung der nichtlinearen
Up: Zeitkontinuierliche Simulierung und Simulation
Previous: Grundlagen der numerischen Simulation
Contents
Index
Marco Möller 17:20:55 24.10.2005