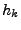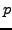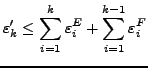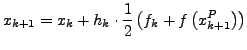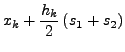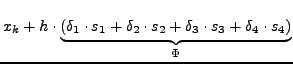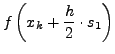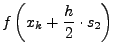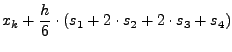Next: Integration von Zustands-DGLn mit
Up: Zeitkontinuierliche Simulierung und Simulation
Previous: Berechnung nichtlinearer Gleichgewichtslösungen
Contents
Index
Subsections
- Bahn
- (Pfad, Weg) kontinuierlich, räumliche Punktfolge
- Trajektorie
- Bahn mit ``zeitlichen Beschränkungen''
- z.B. außer Position auch Geschwindigkeit (und Beschleunigung) an jedem
Punkt der Bahn (evtl. Impliziet über
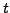 Achse) gegeben
Achse) gegeben
- Einsatzgebiet
- der numerischen Lösung überall dort wo nichtlinearitäten
vorliegen bzw. keine expliziete Lösung gefunden wird (werden kann)
Klassen Numerischer Integrationsverfahren
jeweils explizit und implizit:
- Einschrittverfahren - nur diese sind hier erwähnt
- Mehrschrittverfahren
- Extrapolationsverfahren
Kriterien für Integratorenwahl
- Rechenaufwand (Berechnungseffizienz)
- Genauigkeit (Approximationsfehler)
- Eignung für steife Systeme (Stabilität). Bei steifen DGL impliziete
Verfahren bevorzugen!
- Implementierungsaufwand (Eigenprogrammierung oder Verwendung einer
Bibliothek)
Ordnung des Verfahrens
(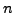 )
)
Einschrittverfahren
- Gegeben
-
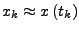
- Gesucht
-
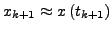
- Ansatz
- für Einschrittverfahren
- Konsistenzbedingung
- für Einschrittverfahren
Explizites Euler Verfahren
- Rechenaufwand gering, nur 1 Auswertung pro Schritt. Für Echtzeitsysteme
interessant
- Genauigkeit: Approximationsfehler
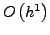
- Für hohe Genauigkeiten kleine Schrittweite nötig
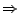 Stabilitätsprobleme
Stabilitätsprobleme
- Schrittweite
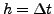
- Gesamtfehler
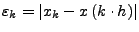
- Bei zu kleiner Schrittweite dominieren Rundungsfehler
- Bei zu großer Schrittweite dominieren Einzelschritt- und Fortpfanzungsfehler
-
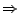 Notwendigkeit für Adaptive Schrittweitensteuerung
Notwendigkeit für Adaptive Schrittweitensteuerung
- Einzelschritt- und Fortpflanzungsfehler
-
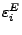 Einzelschrittfehler
Einzelschrittfehler
-
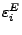 Fortpflanzungsfehler
Fortpflanzungsfehler
Implizites Euler Verfahren
- Ein Verfahrensschritt erfordert die (näherungsweise) Lösung der nichtlinearen
Gleichung
nach
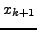
- Rechenaufwand: sehr hoch
- Genauigkeit: Approximatinsfehler
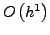
- Für hohe Genauigkeit kleine Schrittweite nötig, aber bessere Stabilitätseigenschaften
als explizites Euler Verfahren
- Ist ein Prädiktor-Korrektor Verfahren
- Prädiktor Schritt:
- Kottektor Schritt: Mittelung des Gradienten
- Insgesamt:
- Ist ein zweistufiges Einzelschrittverfahren - Rechenaufwand zwei Funktionsauswertungen
von
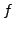
- Genauigkeit: Approximationsfehler
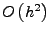
- Heun Verfahren ist
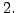 Ordnung
Ordnung
man versucht nun die unbekannten Koeffizienten
so zu bestimmen, dass
- die Konsistenzbedingung
erfüllt ist:
- der Approximationsfehler möglichst klein wird (d.h.
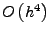
- Rechenaufwand: vier Auswertungen von
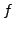
- Genauigkeit: Approximationsfehler
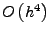
Schrittweitensteuerung
- ungenau, wenn gesuchte Lösung sich lokal sehr stark ändert
- ineffizient, wenn gesuchte Lösung sich lokal sehr wenig ändert
- Wahl von
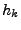 ``so groß wie möglich'' und ``so klein wie
nötig'' und das neu von Schritt zu Schritt
``so groß wie möglich'' und ``so klein wie
nötig'' und das neu von Schritt zu Schritt
- Wahl von
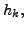 so dass globaler Approximationsfehlers nach einem
Schritt unterhalb einer Fehlerschranke liegt
so dass globaler Approximationsfehlers nach einem
Schritt unterhalb einer Fehlerschranke liegt
- Berechnung von
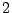 Näherungen für
Näherungen für 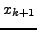 : einmal für Schrittweite
: einmal für Schrittweite
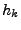 und einmal für Schrittweite
und einmal für Schrittweite
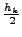
- Daraus Schätzung des lokalen Fehlers
- Anpassung von
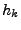 so dass lokale Fehlerschätzung unter Schranke
liegt.
so dass lokale Fehlerschätzung unter Schranke
liegt.
- Aufwand:
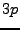 Funktionsauswertungen
Funktionsauswertungen
- z.B.
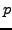 und
und 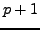
- Berechnung von
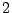 Näherungen für
Näherungen für 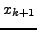 für dieselbe Schrittweite
für dieselbe Schrittweite
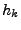
- Bei geeigneter ``Einbettung'' der beiden Verfahren, z.B. Runge-Kutta-Verfahren
4. und 5. Ordnung zusammen nur
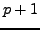 Funktionsauswertungen nötig
Funktionsauswertungen nötig
- Ansatz viel effizienter als ``Einschrittverfahren der Ordnung
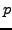 ''
''
- Simulationssprachen
- Simulationsframeworks
- Simulink
- C++ Klassenbibliothek
- Graphische Modellierung
- Simulink
- WorkingModel
- Aspen
- Stella
- Spezialsimulatoren
- Multidisziplinäre Modellgenerierung





Next: Integration von Zustands-DGLn mit
Up: Zeitkontinuierliche Simulierung und Simulation
Previous: Berechnung nichtlinearer Gleichgewichtslösungen
Contents
Index
Marco Möller 17:20:55 24.10.2005