Next: Rechenoperationen mit Matrizen I.190
Up: Formelsammlung Mathe I/II für
Previous: Lineare Abbildungen I.183
Contents
Index
Matrizen I.190
Eine 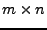 -Matrix ist ein rechteckiges Zahlenschema mit m Zeilen
und n Spalten. Man schreibt
-Matrix ist ein rechteckiges Zahlenschema mit m Zeilen
und n Spalten. Man schreibt
dabei steht 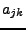 in der j-ten Zeile, und der k-ten Spalte.
in der j-ten Zeile, und der k-ten Spalte.
Zeilen- und Spaltenvektor
I.191
Einem 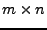 -Matrix hat
-Matrix hat 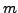 Zeilenvektoren (aus der
Zeilenvektoren (aus der 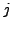 -ten
Zeile):
-ten
Zeile):
und 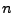 Spaltenvektoren (aus der
Spaltenvektoren (aus der 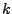 -ten Spalte):
-ten Spalte):
- Zeilenvektoren können als eine
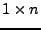 -Matrix angesehen werden
-Matrix angesehen werden
- Spaltenvektoren können als eine
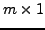 -Matrix angesehen werden
-Matrix angesehen werden
Die Menge aller 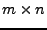 -Matrizen über
-Matrizen über
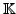 bildet zusammen
mit der Addition und der Skalarmultiplikation einen Vektorraum
über
bildet zusammen
mit der Addition und der Skalarmultiplikation einen Vektorraum
über
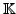 der Dimension
der Dimension 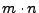 .
.
Subsections
Marco Möller 17:42:11 24.10.2005
![]() -Matrix ist ein rechteckiges Zahlenschema mit m Zeilen
und n Spalten. Man schreibt
-Matrix ist ein rechteckiges Zahlenschema mit m Zeilen
und n Spalten. Man schreibt 
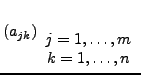
![]() -Matrix hat
-Matrix hat ![]() Zeilenvektoren (aus der
Zeilenvektoren (aus der ![]() -ten
Zeile):
-ten
Zeile):