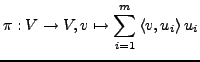Next: Fourierreihe
Up: Euklidische und unitäre Vektorräume
Previous: Orthonormalbasen
Contents
Index
Subsections
Sei
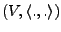 euklidischer
oder unitärer Raum.
euklidischer
oder unitärer Raum.
Zu
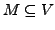 heißt
heißt
das orthogonale Komplement
von 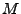 .
.
-
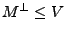 ist linearer Teilraum von
ist linearer Teilraum von 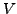
Seien
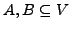 . Dann gilt:
. Dann gilt:
-
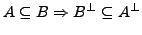
-
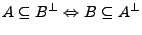
-
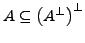
-
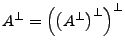
-
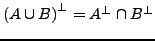
-
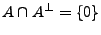
Sei
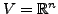 euklidischer Raum und
euklidischer Raum und
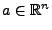 .
Dann ist für
.
Dann ist für
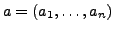 und
und
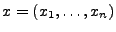
die Lösungemenge der linearen Gleichung
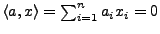 .
.
Weiterhin gilt für
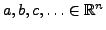 , dass
, dass
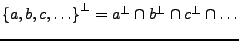 die Lösungsmenge des homogenen linearen Gleichungsystems
die Lösungsmenge des homogenen linearen Gleichungsystems
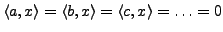
- für
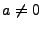 ist
ist 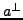 eine lineare Hyperebene
eine lineare Hyperebene
-
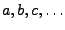 sind sozusagen die Zeilen der Matrix des zugehörigen
linearen Gleichungsystems
sind sozusagen die Zeilen der Matrix des zugehörigen
linearen Gleichungsystems
Sei
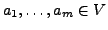 und
und
dann gilt
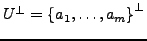 .
.
Sei 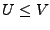 endlich dimensionaler Teilraum. Dann gelten
endlich dimensionaler Teilraum. Dann gelten
-
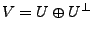
-
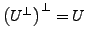
Projektion
Sei 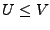 ein endlichdimensionaler Teilraum mit Orthonormalbasis
ein endlichdimensionaler Teilraum mit Orthonormalbasis
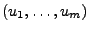 . Die Abbildung
. Die Abbildung
besitzt folgende Eigenschaften:
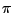 ist linear
ist linear
-
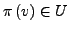 für alle
für alle 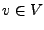
-
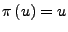 für alle
für alle 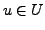
-
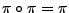
d.h. 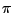 ist eine Projektion auf
ist eine Projektion auf 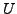
-
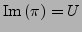 und
und
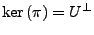
-
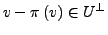 für alle
für alle 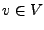
-
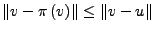 für alle
für alle
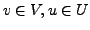
Gleichheit gilt nur für
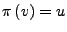 .
.





Next: Fourierreihe
Up: Euklidische und unitäre Vektorräume
Previous: Orthonormalbasen
Contents
Index
Marco Möller 20:09:10 02.12.2005
![]() euklidischer
oder unitärer Raum.
euklidischer
oder unitärer Raum.
![]() heißt
heißt
![]() . Dann gilt:
. Dann gilt:
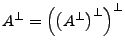
![]() euklidischer Raum und
euklidischer Raum und
![]() .
Dann ist für
.
Dann ist für
![]() und
und
![]()
![]() , dass
, dass
![]() die Lösungsmenge des homogenen linearen Gleichungsystems
die Lösungsmenge des homogenen linearen Gleichungsystems
![]()
![]() und
und
![]() endlich dimensionaler Teilraum. Dann gelten
endlich dimensionaler Teilraum. Dann gelten
![]() ein endlichdimensionaler Teilraum mit Orthonormalbasis
ein endlichdimensionaler Teilraum mit Orthonormalbasis
![]() . Die Abbildung
. Die Abbildung