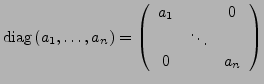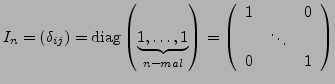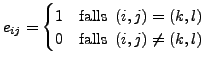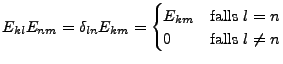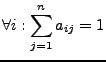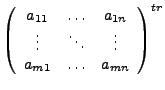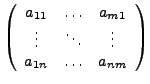Next: Strukturen linearer Abbildungen
Up: Vektroräume
Previous: Summen in Vektorräumen
Contents
Index
Subsections
Seien  und
und 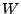 Vektorräume über demselben Körper
Vektorräume über demselben Körper  .
.
Eine Abbildung
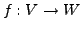 heißt linear
(über
heißt linear
(über  ), falls gilt:
), falls gilt:
Sei
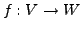 lineare Abbildung. Die Menge
lineare Abbildung. Die Menge
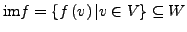 heißt Bild von
heißt Bild von 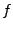 .
.
Die Menge
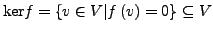 heißt Kern von
heißt Kern von 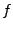 .
.
- Es gilt immer
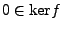
- Der Kern ist ein Untervektorraum von
 :
:
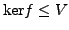
- Das Bild ist ein Untervektorraum von
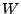 :
:
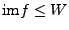
- Das Urbild ist ein Untervektorraum:
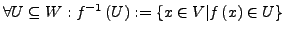
- Eine lineare Abbildung ist injektiv genau dann, wenn
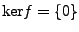 ist
ist
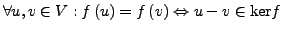
- Die Basis des Bildes entspricht den nicht 0 Zeilen nach anwendung
von Gauss-Jordan auf
![$ \left[\varphi\right]^{Tr}$](img259.png)
- Eine lineare Abbildung wird auch als Vektorraum Homomorphismus (strukturerhaltende
Abbildung) bezeichnet
Eine Abbildung, für die gilt
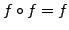 , nennt man eine Projektion.
, nennt man eine Projektion.
- Für eine lineare Abbildung
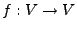 , die eine Projektion
ist, gilt
, die eine Projektion
ist, gilt
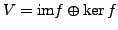
- für
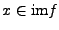 gilt:
gilt:
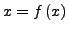
- Ist
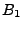 eine Basis von
eine Basis von
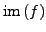 und
und 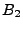 eine Basis von
eine Basis von
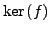 so ist die Matrix von
so ist die Matrix von
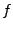 bezüglich
bezüglich
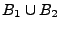 eine Diagonalmatrix, auf deren Diagonalen
nur Nullen und einsen stehen.
eine Diagonalmatrix, auf deren Diagonalen
nur Nullen und einsen stehen.
-
![$ \left[f\right]$](img270.png) ist ähnlich zu einer Diagonalmatrix, es gibt also
ein
ist ähnlich zu einer Diagonalmatrix, es gibt also
ein 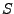 , so dass
, so dass
![$ S^{-1}\left[f\right]S$](img272.png) eine Diagonalmatix ist.
eine Diagonalmatix ist.
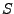 ist die Basismatirix von
ist die Basismatirix von
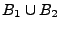 .
.
Dimensionsformel
Für das Folgende erweitern wir die Addition in
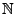 auf die
Menge
auf die
Menge
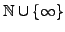 wie folgt:
wie folgt:
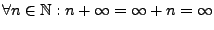 .
.
Sei
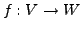 eine lineare Abbildung.
eine lineare Abbildung.
Es gilt
- Beachten dass alle Dimensionen bzgl. gleichem Körper messen.
-
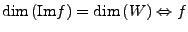 surjektiv
surjektiv
-
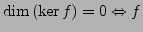 injektiv
injektiv
Sei
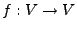 linear und
linear und
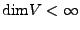 . Dann sind
Injektivität, Surjektivität
und Bijektivität äquivalent.
. Dann sind
Injektivität, Surjektivität
und Bijektivität äquivalent.
- Bei unendlich dimensionalen Vektorräumen sind gilt die Äquivalenz
von In-, Sur- und Bijektivität nicht.
Sei
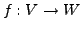 linear.
linear.
heißt Rang von 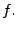
Sei
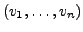 Basis von
Basis von  und
und
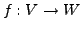 lineare Abbildung. Es gilt:
lineare Abbildung. Es gilt:
-
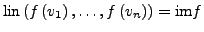
-
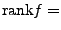 maximale Länge einer linear unabhängigen Teilfamilie
von
maximale Länge einer linear unabhängigen Teilfamilie
von
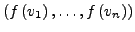
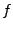 surjektiv
surjektiv
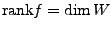
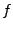 injektiv
injektiv
 linear unabhängig
linear unabhängig
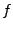 bijektiv
bijektiv
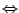
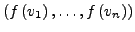 Basis von
Basis von 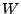
Hauptsatz über lineare Abbildungen
Seien 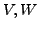
 -Vektorräume,
-Vektorräume,
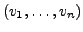 Basis von
Basis von  und
und
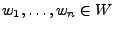 . Dann existiert genau
eine lineare Abbildung
. Dann existiert genau
eine lineare Abbildung
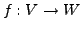 mit
mit
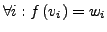
Eine bijektive  -lineare Abbildung heißt
-lineare Abbildung heißt  -Vektorraum-Isomorphismus.
-Vektorraum-Isomorphismus.
Zwei  -Vektorräume
-Vektorräume 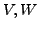 heißen isomorph,
falls ein
heißen isomorph,
falls ein  -Vektorraum-Isomorphismus
-Vektorraum-Isomorphismus
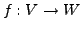 existiert.
existiert.
Sei  ein
ein 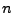 -dimensionaler
-dimensionaler  -Vektorraum mit
-Vektorraum mit 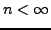 . Dann
ist
. Dann
ist  isomorph zu
isomorph zu 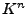 .
.
Sei 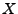 eine Menge und
eine Menge und
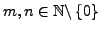 .
Eine
.
Eine
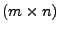 -Matrix
-Matrix 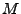 mit Koeffizienten
in
mit Koeffizienten
in 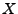 ist eine Abbildung
ist eine Abbildung
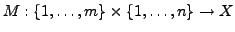 .
Üblicherweise schreibt man so ein
.
Üblicherweise schreibt man so ein 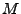 als rechteckiges Schema.
als rechteckiges Schema.
- Merkregel für die Indizes:
Zeilen Zuerst - Spalten Später
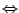 1.ter Index für
Zeilennummer, 2.ter Index für Spaltennummer
1.ter Index für
Zeilennummer, 2.ter Index für Spaltennummer
Abbildungsmatrix
Sei 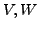 Vektorräume über
Vektorräume über  und
und
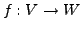 eine lineare
Abbildung. Seien
eine lineare
Abbildung. Seien
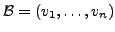 und
und
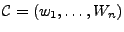 Basen von
Basen von  bzw.
bzw.
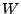 . Für jedes
. Für jedes
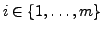 existiert eindeutig
bestimmte
existiert eindeutig
bestimmte
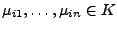 mit
mit
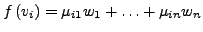 .
Die Matrix
.
Die Matrix
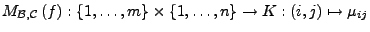 heißt Matrix von
heißt Matrix von 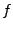 bzgl.
bzgl.
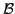 und
und
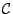 .
.
- In den Spalten einer Matirx stehen die Bilder der Basisvektoren bezüglich
der zugehörigen linearen Abbildung.
Besondere Matrizen
Diagonalmatrix
- Sind invertierbar mit
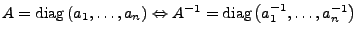
Einheitsmatrix
-
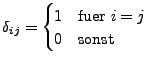 ist das Kronecker Symbol.
ist das Kronecker Symbol.
- sind multiplikativ neutrales Element der Matrizen.
Elementarmatrizen
-
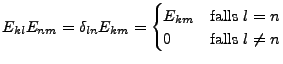
- spannen den Vektorraum der Matrizen auf, sind also eine Basis
- Permutationsmatrix
-
- Entspicht einer Matrix die auf der Diagonalen nur 1en und sonst 0en
hat, bis auf zwei stellen, bei der diese mit mit den 0en auf der Nebendiagonale
vertauscht wurden.
- Multiplikation bewirkt Vertauschung zweier Spalten
- Ist inertierbar (ist selbst ihre eigene Inverse)
- Stochastische Matrix
-
- Das Produkt von stochastischen Matrizen ist wieder eine stochastische
Matrix
- Transposition
-
- Nilpotent
-
Eine Matrix
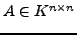 heißt nilpotent, falls ein
heißt nilpotent, falls ein
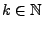 existiert mit
existiert mit
- Nilpotente Matrizen nur 0 als Eigenwert





Next: Strukturen linearer Abbildungen
Up: Vektroräume
Previous: Summen in Vektorräumen
Contents
Index
Marco Möller 20:09:10 02.12.2005
![]() und
und ![]() Vektorräume über demselben Körper
Vektorräume über demselben Körper ![]() .
.
![]() heißt linear
(über
heißt linear
(über ![]() ), falls gilt:
), falls gilt:
![]() lineare Abbildung. Die Menge
lineare Abbildung. Die Menge
![]() heißt Bild von
heißt Bild von ![]() .
.
![]() heißt Kern von
heißt Kern von ![]() .
.
![]() , nennt man eine Projektion.
, nennt man eine Projektion.
![]() auf die
Menge
auf die
Menge
![]() wie folgt:
wie folgt:
![]() .
.
![]() eine lineare Abbildung.
eine lineare Abbildung.
![]() linear und
linear und
![]() . Dann sind
Injektivität, Surjektivität
und Bijektivität äquivalent.
. Dann sind
Injektivität, Surjektivität
und Bijektivität äquivalent.
![]() linear.
linear.
![]() Basis von
Basis von ![]() und
und
![]() lineare Abbildung. Es gilt:
lineare Abbildung. Es gilt:
![]()
![]() -Vektorräume,
-Vektorräume,
![]() Basis von
Basis von ![]() und
und
![]() . Dann existiert genau
eine lineare Abbildung
. Dann existiert genau
eine lineare Abbildung
![]() mit
mit
![]()
![]() -lineare Abbildung heißt
-lineare Abbildung heißt ![]() -Vektorraum-Isomorphismus.
-Vektorraum-Isomorphismus.
![]() -Vektorräume
-Vektorräume ![]() heißen isomorph,
falls ein
heißen isomorph,
falls ein ![]() -Vektorraum-Isomorphismus
-Vektorraum-Isomorphismus
![]() existiert.
existiert.
![]() ein
ein ![]() -dimensionaler
-dimensionaler ![]() -Vektorraum mit
-Vektorraum mit ![]() . Dann
ist
. Dann
ist ![]() isomorph zu
isomorph zu ![]() .
.
![]() eine Menge und
eine Menge und
![]() .
Eine
.
Eine
![]() -Matrix
-Matrix ![]() mit Koeffizienten
in
mit Koeffizienten
in ![]() ist eine Abbildung
ist eine Abbildung
![]() .
Üblicherweise schreibt man so ein
.
Üblicherweise schreibt man so ein ![]() als rechteckiges Schema.
als rechteckiges Schema.
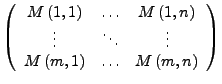
![]() Vektorräume über
Vektorräume über ![]() und
und
![]() eine lineare
Abbildung. Seien
eine lineare
Abbildung. Seien
![]() und
und
![]() Basen von
Basen von ![]() bzw.
bzw.
![]() . Für jedes
. Für jedes
![]() existiert eindeutig
bestimmte
existiert eindeutig
bestimmte
![]() mit
mit
![]() .
Die Matrix
.
Die Matrix
![]() heißt Matrix von
heißt Matrix von ![]() bzgl.
bzgl.
![]() und
und
![]() .
.