Strukturen linearer Abbildungen

Vektorraum aller linearer Abbildungen

Seien $V,W$ $K$-Vektorräume. Die Menge aller linearer Abbildungen $\textrm{Hom}\left(V,W\right)=\left\{ \varphi\in W^{V}\vert\varphi\textrm{ linear}\right\} \le W^{V}$ ist ein Untervektorraum der Menge aller Abbildungen.

• d.h daß die Summer zweier linerarer Abbildungen, und das Produkt mit einem Skalar wieder eine lineare Abbildung ist
• Hom steht für Homomorphismus, das bedeutet, dass dies stukturerhaltene Abbildungen sind.
• Für zwei lineare Abbildungen $\varphi\in\textrm{Hom}\left(U,V\right)$ und $\psi\in\textrm{Hom}\left(V,W\right)$ gilt, das auch die Komposition $\psi\circ\varphi\in\textrm{Hom}\left(U,W\right)$ wieder eine lineare Abbildung ist.
• Wenn $\varphi\in\textrm{Hom}\left(V,W\right)$ bijektiv ist, ist die Umkehrabbildung $\varphi^{-1}\in\textrm{Hom}\left(W,V\right)$ ebenfalls linear und bijektiv.

Ring mit $1$ von linearen Abbildungen / Algebra

Unter $\textrm{End}\left(V\right)=\textrm{Hom}\left(V,V\right)$ versteht man die Menge aller linearen Abbildungen von $V$ in sich selbst. Diese Menge bildet zusammen mit der Addition und der Komposition $\left(\textrm{End}\left(V\right),+,\circ\right)$ einen Ring mit $1$ (siehe Ring mit 1).

Es gelten sogar allgemeiner folgende Rechenregeln. Seien $\forall\varphi,\varphi_{1},\varphi_{2}\in\textrm{Hom}\left(U,V\right)$, $\psi,\psi_{1},\psi_{2}\in\textrm{Hom}\left(V,W\right)$ und $\lambda\in K$

1. $\psi\circ\left(\varphi_{1}+\varphi_{2}\right)=\psi\circ\varphi_{1}+\psi\circ\varphi_{2}$
2. $\left(\psi_{1}+\psi_{2}\right)\circ\varphi=\psi_{1}\circ\varphi+\psi_{2}\circ\varphi$
3. $\left(\lambda\cdot\psi\right)\circ\varphi=\psi\circ\left(\lambda\cdot\varphi\right)=\lambda\cdot\left(\psi\circ\varphi\right)$

Durch die letzte Rechenregel bildet $\left(\textrm{End}\left(V\right),+,\circ\right)$ sogar eine $K$-Algebra.

• Das $1$ Element ist hierbei die Identität: $\textrm{id}:V\rightarrow V$ ist linear
• End steht für Endomorphismus

invertierbare lineare Abbildungen / Gruppe

Unter der general linear group $\textrm{GL}\left(V\right)=\left\{ \varphi\in\textrm{End}\left(V\right)\vert\varphi\textrm{ invertierbar}\right\}$ versteht man die Menge der invertierbaren linearen Abbildungen. Diese bilden bezüglich der Komposition $\circ:\textrm{GL}\left(V\right)^{2}\rightarrow\textrm{GL}\left(V\right)$ und der Identität als $1$ Element eine Gruppe $\left(\textrm{GL}\left(V\right),\circ,\textrm{id}_{V}\right)$.

Verknüpfungen zwischen Matrizen und deren Strukturen

$K^{m\times n}$ ist die Menger aller $m\times n$ Matrizen über $K$. Die quadratischen $n\times n$ Matrizen erhalten das Symbol $M_{n}\left(K\right)=K^{n\times n}$.

Für zwei Matizen $A,B\in K^{m\times n}$ und einen Skalar $\lambda\in K$ sind folgende Verknüpfungen definiert.

$$A+B = \left(a_{ij}\right)+\left(b_{ij}\right)=\left(a_{ij}+b_{ij}\right)$$

$$\lambda A = \lambda\left(a_{ij}\right)=\left(\lambda a_{ij}\right)$$

$K^{m\times n}$ bildet zusammen mit der Addition und Skalarmultiplikation einen Vektorraum.

Seien $A\in K^{m\times n}$ und $B\in K^{n\times k}$. Die Matrixmultiplikation ist wie folgt definiert:

$$C = AB\in K^{m\times k}$$

$$= \left(c_{ij}\right)$$

$$= \left(\sum_{k=1}^{n}a_{ik}b_{kj}\right)$$

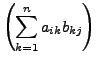Es gelten folgende Rechenregeln: für $A,A_{1},A_{2}\in K^{m\times n}$, $B,B_{1},B_{2}\in K^{n\times k}$und $\lambda\in K$

1. $A\left(B_{1}+B_{2}\right)=AB_{1}+AB_{2}$
2. $\left(A_{1}+A_{2}\right)B=A_{1}B+A_{2}B$
3. $\left(\lambda A\right)B=\lambda\left(AB\right)=A\left(\lambda B\right)$

$\left(M_{n}\left(K\right),+,\cdot\right)$ ist ein Ring mit $1$, diese $1$ ist hier $I_{n}$.

$\textrm{GL}_{n}\left(K\right)=\left\{ A\in M_{n}\left(K\right)\vert A\textrm{ invertierbar}\right\}$ ist die Menge der invertierbaren quadratischen $n\times n$ Matrizen. Diese bildet bezüglich der Matrixmultiplikation eine Gruppe.

• Merkregel für Matrixprodukt: Zelle einer Ergebnisszelle ist ensprechende Zeile der ersten mal Spalte der zweiten Matrix.
• Die Matrixmultiplikation ist assoziativ, d.h. $A\left(BC\right)=\left(AB\right)C$
• Die Matrixmultiplikation ist im allgemeinen nicht kommutativ: $AB\neq BA$
• Spaltenvektoren können als $n\times1$ Marix aufgefasst werden. Es gilt also $K^{n}=K^{n\times1}$
• Das multiplizieren mit einer Matrix aus $\textrm{GL}_{n}\left(K\right)$ ändert den Rang einer Matrix nicht
• der Vektorraum $K^{n\times m}$ wird von den Elementarmatrizen erzeugt.
• $\left(AB\right)^{-1}=B^{-1}A^{-1}$
• $\left(A^{T}\right)^{-1}=\left(A^{-1}\right)^{T}$

Lineare Abbildungen und Matrizen

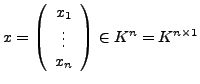Sei $K$ ein Körper, $A=\left(a_{ij}\right)\in K^{m\times n}$ und $x=\left(\begin{array}{c} x_{1}\\ \vdots\\ x_{n}\end{array}\right)\in K^{n}=K^{n\times1}$. Wir definieren

$$\varphi_{A}\left(x\right):K^{n}\rightarrow K^{m}:x\mapsto Ax$$

$$Ax=\left(\begin{array}{ccc} a_{11} & \ldots & a_{1n}\\ \vdots & ... ...{array}\right)\left(\begin{array}{c} x_{1}\\ \vdots\\ x_{n}\end{array}\right)$$

$$=\left(\begin{array}{c} a_{11}x_{1}+\ldots+a_{1n}x_{n}\\ \vdots\\ a_{m1}x_{1}+\ldots+a_{mn}x_{n}\end{array}\right)$$

als die zur Matrix $A$ gehörende lineare Abbildung.

• Es gilt: $\forall i\in\left\{ 1,\ldots,n\right\} :\varphi_{A}\left(e_{i}\right)=\left(\begin{array}{c} a_{1i}\\ \vdots\\ a_{mi}\end{array}\right)$
  Das heißt, dass die Spalten einer Matrix die Bilder der Standardbasisvektoren enthält.
• Das Bild von $\textrm{Im}\varphi_{A}=\textrm{lin}\left(\varphi_{A}\left(e_{1}\right),\ldots,\varphi_{A}\left(e_{n}\right)\right)=$ Unterraum von $K^{m}$, der von den Spalten von $A$ aufgespannt wird. Diesen Raum nennt man auch Spaltenraum von $A$.

Blockmatrizen

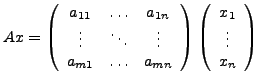
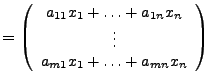
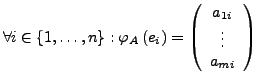
Die Elemente einer Matrix können wiederum Matrizen sein, sogenannte Blockmatrizen. Andererseit lässt kann man sich dies so Vorstellen, als ob Blöcke innerhalb der Matrix als Untermatrix aufgefasst werden. Hiermit ergeben sich (bei passenden Größen) folgende Rechenregeln.

• Im grunde Identisch, als ob die Elemente keine Matrizen wären, z.B.:

$$\left(\begin{array}{cc} A_{11} & A_{12}\\ A_{21} & A_{22}\end{ar... ...t)\left(\begin{array}{cc} B_{11} & B_{12}\\ B_{21} & B_{22}\end{array}\right)=$$

$$\left(\begin{array}{cc} A_{11}B_{11}+A_{12}B_{21} & A_{11}B_{12}+... ...{22}\\ A_{21}B_{11}+A_{22}B_{21} & A_{21}B_{12}+A_{22}B_{22}\end{array}\right)$$

Rang einer Matrix

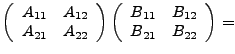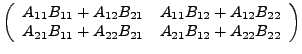Unter den Rank einer Matrix $A\in K^{m\times n}$ versteht man

$$\textrm{rank}_{K}A = \textrm{rank}_{K}\varphi_{A}$$

$$= \dim_{K}\textrm{lin}\left(\varphi_{A}\left(e_{1}\right),\ldots,\varphi_{A}\left(e_{n}\right)\right)$$

Dieser lässt sich am besten mit Hilfe des Gauß-Jordan-Algorithmus berechnen. Hierzu das Gleichungssystem $Ax=0$ betrachten, und den Rank (Anzahl von nicht Null Spalten in Zeilenstufenform) errechnen. Siehe sub:Gauss-Jordan.

• Das multiplizieren mit einer Matrix aus $\textrm{GL}_{n}\left(K\right)$ (bijektive Abbildung) ändert den Rang einer Matrix nicht
• $\textrm{rank}\left(AA^{T}\right)=\textrm{rank}\left(A\right)$
• $\textrm{rank}\left(A^{T}\right)=\textrm{rank}\left(A\right)$

$K$-Algebra Isomorphismus

Die Abbildung $\Phi:K^{m\times n}\rightarrow\textrm{Hom}\left(K^{n},K^{m}\right):M\mapsto\varphi_{M}$ ist ein linearer Isomorphismus. Die Abbildung $\Phi$ ordnet einer Matrix $M\in K^{m\times n}$ eine lineare Abbildung $\varphi_{M}:K^{n}\rightarrow K^{m}$ zu. Die inverse Abbildung $\Phi^{-1}:\textrm{Hom}\left(K^{n},K^{m}\right)\rightarrow K^{m\times n}:\varphi\mapsto$ ordnet einer linearen Abbilung $\varphi:K^{n}\rightarrow K^{m}$ die Matrix $\left[\varphi\right]$ von $\varphi$ bezüglich der Standardbasis von $K^{n}$ bzw. $K^{m}$ zu.

• $\varphi_{A}\circ\varphi_{B}=\varphi_{A\cdot B}$
  $\left[\varphi\circ\psi\right]=\left[\varphi\right]\cdot\left[\psi\right]$
• $\varphi_{\lambda\cdot A}=\lambda\varphi_{A}$
  $\left[\lambda\varphi\right]=\lambda\left[\varphi\right]$
• $\varphi_{A+B}=\varphi_{A}+\varphi_{B}$
  $\left[\varphi+\psi\right]=\left[\varphi\right]+\left[\psi\right]$
• $\varphi_{I_{n}}=\textrm{id}$
  $\left[\textrm{id}\right]=I_{n}$